| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 하둡2
- Java
- C
- graph
- yarn
- collections
- 딥러닝
- recursion
- 코딩더매트릭스
- python
- hadoop2
- 주식분석
- 알고리즘
- RNN
- GRU
- LSTM
- C언어
- 하이브
- NumPy
- scrapy
- codingthematrix
- 텐서플로
- HelloWorld
- tensorflow
- hive
- 선형대수
- 그래프이론
- effective python
- 파이썬
- Sort
- Today
- Total
목록Linear Algebra/Coding the Matrix (11)
EXCELSIOR
 [코딩더매트릭스]Chap10 - 직교화 Orthogonalization
[코딩더매트릭스]Chap10 - 직교화 Orthogonalization
Chap 10직교화(Orthogonalization)이번 장의 첫 번째 목적은 다음 문제에 대한 알고리즘을 제시하는 것이다.Computational Problem : (여러 벡터들의 Span 내에 있는 가장 가까운점 ) 주어진 벡터 와 실수 벡터들 에 대해, Span 내에 있으며 에서 가장 가까운 벡터를 찾아보자. 라 하고, 행렬-벡터 곱셈의 선형결합 정의에 의하면, Span 내 벡터들의 집합은 로 표현할 수 있는 벡터들의 집합이다. 따라서, 결국 계수(좌표)들을 찾는 것은 을 최소화 하는 벡터 를 찾는 것과 같다. 이것을 최소제곱 (least-squares) 문제라고 한다.10.1 복수의 벡터들에 직교하는 투영9장에서 살펴보았던 소방차 문제 와 같이 직교성과 투영(proj..
 [코딩더매트릭스]Chap09 - 내적 Inner Product
[코딩더매트릭스]Chap09 - 내적 Inner Product
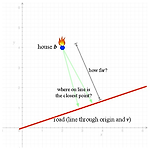
Chap 09내적 - Inner Product이번 9장에서는 길이 (length)와 직교 (perpendicular)의 개념이 수학적 용어로 어떻게 해석되는지 알아본다. 어떤 점에 가장 가까운 주어진 직선상의 점을 찾는 문제에 대해 살펴본다. 9.1 소방차 문제아래의 그림에서 좌표 에 위치한 집 에 화재가 났다고 하자. 집 주변을 지나가는 도로는 원점과 점 을 지나는 직선이면, 집 와 가장 가까운 직선상의 어떤 지점으로 소방차를 위치 시킬 수 있으면 화재를 진압 시킬 수 있다고 하면, 두 가지를 생각할 수 있다.직선상의 어느 점이 집 와 가까운가?그렇다면, 가장 가까운 거리는 얼마나 되는가? 이것을 계산문제로 재구성 해보자. 앞의 3.5.3 에서 처럼 원점을 지나는 직선은 벡터의 스칼라배들의..
Chap 08가우스 소거법 - Gaussian Elimination가우스 소거법(Gaussian Elimination)은 선형방정식의 시스템에 대한 해를 구하는 데에 가장 자주 적용된다. 가우스 소거법은 주로 아래와 같은 곳에 적용된다.주어진 벡터들의 생성에 대한 기저 찾기행렬의 영공간에 대한 기저 찾기행렬방정식의 해 구하기 8.1 사다리꼴 - Echelon Form사다리꼴(Echelon form) 행렬은 삼각행렬을 일반화한 것이다. 아래의 행렬은 사다리꼴 행렬의 예시이다.행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.Definition : ..
Chap 07차원 - Dimension 7.1 기저의 크기7.1.1 Morphing 보조 정리와 그 응용Lemma (Morphing Lemma) : 는 벡터공간이라고 하자. 는 에 대한 생성자들의 집합이라 하고, 는 에 속하는 벡터들로 구성된 선형독립인 집합(즉, 기저)이라고 하면, 이다. Theorem (Basis Theorem) : 는 벡터공간이라 하고, 에 대한 모든 기저(basis)는 동일한 크기를 가진다.Proof : 과 는 에 대한 두 기저라고 하자. 과 를 위의 Morphing Lemma 에 적용하면 라고 할 수 있다. 와 을 적용하면 이다. 이 둘의 부등식을 결합하면 를 얻을 수 있다. Theorem : 는 벡터공간이라고 ..
Chapter 06기저 - Basis6.1 좌표계 - Coordinate system6.1.1 데카르트의 생각1618년 프랑스의 수학자 르네 데카르트(René Descartes)는 기하학을 접근하는 방식을 완전히 바꾼 개념을 발견하였다. 일화에 따르면 데카르트는 침대에 누워 방의 천장 모서리 주위를 날고 있는 파리를 보고 있다가 기하학에 대한 훌륭한 생각이 떠올랐다고 한다. (역시 천재는 생각하는 자체가 다른듯...) 데카르트는 파리의 위치는 두 개의 숫자, 즉 파리 근처 두 개의 벽으로부터 파리까지의 거리로 기술할 수 있다는 것을 깨달았고, 두 벽이 수직이 아니라도 이것이 사실이라는 것을 알게 되었다. 또한 데카르트는 기하학적 분석을 대수적으로 접근할 수 있음을 알게 되었다. (엄청나다...) 6.1...
깃헙으로 Jupyter Notebook을 볼 경우 LaTex 문법이 깨지는 경우가 있어 되도록 nbviewer로 보는 것을 추천한다. nbviewer에서 보기Chap 05 - 행렬(The Matrix)5.1 행렬이란 무엇인가?5.1.1 전통적인 행렬일반적으로, 개의 행과 개의 열을 가진 행렬은 행렬이라 한다. 행렬 에 대해 원소 는 번쨰 행과 번째 열에 있는 원소로 정의되며, 전통적으로 또는 로 나타낸다. 따라서, 상의 모든 과 에 대하여 일 때,을 -위의 ()-행렬(()-matrix over )이라고 한다. 5.1.2 행렬에 대해 알아보기상의 -벡터를 집합 에서 로의 함수로 정의한거 처럼, 상의 행렬을 카테시안 곱 로의 함수로 정의한다. 의 원소를..
해당 포스팅을 Nbviewer 에서 보는 것을 추천한다. Nbviewer로 보기 4.1 선형결합(일차결합) - Linear combination4.1.1 선형결합의 정의Definition 4.1.1 : 각각을 벡터라고 하면, 의 선형결합 을 다음과 같은 합이라고 정의하자.여기서, 은 스칼라이다. 이 선형결합에서 각각은 계수라고 한다. 은 의 계수이고, 는 의 계수이며, ..., 은 의 계수이다.4.1.2 선형결합의 사용Example 4.1.5 평균얼굴 - p.126 이미지의 평균을 선형결합으로 나타낼 수 있다. import numpy as np import matplotlib.pyplot as plt from PIL import Image # 이미지 파일 불러오기 u =..
해당 포스팅을 Nbviewer 에서 보는 것을 추천한다. Nbviewer로 보기 3.1 벡터란 무엇인가?벡터란 단어는 "vehere(운반하다)"라는 뜻의 라틴어에서 유래되었다. 어떤 것을 한 장소에서 다른 곳으로 이동하는 벡터의 방향성을 내포하고 있다. 한 벡터의 모든 원소는 하나의 필드 (Chap02 참고)에서 나와야 한다.Definition 1 : 필드 와 양의 정수 에 대해, 에 속하는 개의 원소를 가지는 벡터를 상의 -벡터라고 한다. 상의 -벡터들의 집합은 으로 나타낸다. 예를 들어, 아래의 (실수) 상의 4-벡터들의 집합을 라고 쓴다.위의 4-벡터 집합을 함수로 생각하면 를 함수의 집합에 대한 표기법으로 해석할 수 있다. 따라서, 위의 4-벡터는 사실상 함수라고 할 ..
