| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 코딩더매트릭스
- LSTM
- tensorflow
- effective python
- recursion
- 하둡2
- 딥러닝
- HelloWorld
- 하이브
- NumPy
- GRU
- 주식분석
- collections
- python
- graph
- codingthematrix
- 텐서플로
- hadoop2
- Java
- C
- Sort
- 그래프이론
- 파이썬
- C언어
- scrapy
- 알고리즘
- RNN
- hive
- yarn
- 선형대수
- Today
- Total
EXCELSIOR
[코딩더매트릭스]Chap08 - 가우스 소거법 Gaussian Elimination 본문
[코딩더매트릭스]Chap08 - 가우스 소거법 Gaussian Elimination
Excelsior-JH 2018. 5. 4. 09:44가우스 소거법 - Gaussian Elimination
가우스 소거법(Gaussian Elimination)은 선형방정식의 시스템에 대한 해를 구하는 데에 가장 자주 적용된다. 가우스 소거법은 주로 아래와 같은 곳에 적용된다.
주어진 벡터들의 생성에 대한 기저 찾기
행렬의 영공간에 대한 기저 찾기
행렬방정식의 해 구하기
8.1 사다리꼴 - Echelon Form
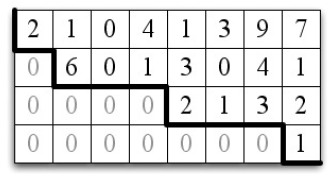
사다리꼴(Echelon form) 행렬은 삼각행렬을 일반화한 것이다. 아래의 행렬은 사다리꼴 행렬의 예시이다.
행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.
행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.
행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.
행 의 첫 번째 영이 아닌 엔트리는 열 에 있다.
Definition : 행렬 는 다음 조건을 만족하면 사다리꼴 이다. 즉, 임의의 행에 대해, 만약 그 행의 첫 번째 영이 아닌 원소가 위치 에 있으면 그 행 이전의 모든 행의 첫 번째 영이 아닌 원소는 보다 작은 어떤 위치에 있다.
즉, 다음과 같은 행렬이 사다리꼴 행렬이라 할 수 있다. ( 은 아무 숫자나 올 수 있다.)
위의 Definition에 의하면 의 각 행에 대해 반복할 때마다 각 행의 첫 번째 영이 아닌 엔트리는 반드시 오른쪽으로 이동하여 오른쪽 아래로 내려가는 계단모양을 형성한다.
만약, 아래의 예시와 같이 사다리꼴 행렬에서 어떤 행이 모두 영이면, 그 행 다음에 오는 모든 행 또한 모두 영이어야 한다.
8.1.1 사다리꼴에서 행공간에 대한 기저로
사다리꼴로 된 행렬이 가지는 장점은 무엇일까?
Lemma : 만약 어떤 행렬이 사다리꼴이면, 영이 아닌 행들은 행공간에 대한 기저를 형성한다.
예를 들어, 다음 행렬
의 행공간에 대한 기저는 이다.
8.1.2 생략
8.1.3 맨 왼쪽의 영이 아닌 위치에 의한 행들의 정렬
모든 행렬이 사다리꼴 형태를 가지는 것은 아니다. 이번 8.1.3에서는 사다리꼴이 아닌 행렬을 사다리꼴 행렬로 변환하는 방법에 대해 알아 보도록 하자.
사다리꼴 행렬은 위의 Definition에서 처럼 맨 왼쪽의 영이 아닌 원소의 위치에 따라 정렬되어야 한다. 아래와 같이 행렬 가 있다고 해보자.
이를 사다리꼴 행렬로 바꾸기 위해서는 행렬 중 행의 성분을 사다리꼴 형태가 되도록 위치를 바꿔주는 피보팅(pivoting)과정이 필요하다. 피보팅 과정을 거치면 아래와 같은 행렬이 된다.
이제 이러한 피보팅 작업을 해주는 과정을 파이썬 코드로 나타내 보자. 아래의 코드는 pivoting()메소드를 구현한 코드이다.
def pivoting(mat):
row_idx = list(range(len(mat)))
col_idx = len(mat[0])
pivot_mat = []
for c in range(col_idx):
rows_with_nonzero = [r for r in row_idx if mat[r][c] != 0]
if rows_with_nonzero:
pivot = rows_with_nonzero[0]
for idx in rows_with_nonzero:
pivot_mat.append(mat[idx])
row_idx.remove(idx)
return pivot_mat
A = [[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[1, 2, 3, 4, 5],
[0, 0, 0, 6, 7],
[0, 0, 0, 9, 9]]
from pprint import pprint
pprint(pivoting(A))
'''출력결과
[[1, 2, 3, 4, 5],
[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[0, 0, 0, 6, 7],
[0, 0, 0, 9, 9]]
'''위의 pivoting 과정을 거쳐 나온 행렬 는 사다리꼴 행렬이라고 할 수 없다. 그 이유는 네 번쨰 행과 다섯 번째 행의 처음으로 영이 아닌 원소는 네 번째 열에 위치하기 때문이다.
8.1.4 기본행덧셈 연산 (Elementary row-addition operation)
이러한 문제를 해결하는 방법으로는 elementary row-addtion operation 이 있다. 영어로 써놔서 엄청 어려운 과정처럼 보이지만, 위의 행렬 에서 사다리꼴 행렬이 되지 않는 원인인 네 번째와, 다섯 번째의 행을 세 번째의 행으로 곱셈과 뺼셈 을 이용해 해당 원소를 으로 만들어 주면 된다.
네 번째 행 은 아래와 같이 세 번째 행 를 이용해 네 번째 열의 원소를 으로 만들어 줄 수 있다.
다섯 번째 행 는,
이된다. 따라서, 아래와 같은 행렬이 얻어진다.
행렬에서 네 번째행을 이용하여,
다섯 번째행을 으로 만들어 주게 되어, 최종적으로 아래와 같은 행렬이 만들어 진다.
위의 elementary row-addition operation 과정을 파이썬 코드로 나타내면 아래와 같다. 아래의 코드는 위에서 본 pivoting()메소드에서 elementary row-addition operation 과정을 추가해준 코드이다.
def row_reduce(mat):
rref = []
row_idx = list(range(len(mat)))
col_idx = len(mat[0])
for c in range(col_idx):
rows_with_nonzero = [r for r in row_idx if mat[r][c] != 0]
if rows_with_nonzero:
pivot = rows_with_nonzero[0]
row_idx.remove(pivot)
rref.append(mat[pivot])
for r in rows_with_nonzero:
if r is not pivot:
multiplier = mat[r][c] / mat[pivot][c]
mat[r] = [a - multiplier*b for a, b in zip(mat[r], mat[pivot])]
for r in row_idx:
rref.append(mat[r])
return rref
mat = [[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[1, 2, 3, 4, 5],
[0, 0, 0, 6, 7],
[0, 0, 0, 9, 9]]
row_reduce(mat)
'''
[[1, 2, 3, 4, 5],
[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[0.0, 0.0, 0.0, 0.0, 3.0],
[0.0, 0.0, 0.0, 0.0, 0.0]]
'''8.1.5 기본행덧셈 행렬에 의한 곱셈
8.1.4에서 보았듯이, 한 행의 배수로 다른 행에서 빼는 것은 그 행렬을 기본행덧셈 행렬(elementary row-addition matrix)과 곱합으로써 구할 수 있다.
8.1.6 행덧셈 연산은 행공간을 유지한다.
행렬을 사다리꼴로 변환하는 목적은 그 행렬의 행공간에 대한 기저를 얻기 위해서 이다. 조금 있다가 살펴보겠지만, 행덧셈 연산은 행공간을 바꾸지 않는다. 따라서, 변환된 행렬(사다리꼴 행렬 )의 행공간에 대한 기저는 원래 행렬에 대한 기저이다.
Lemma : 행렬 와 에 대해, Row Row 이다.
proof : 는 Row 의 임의의 벡터라고 하면, 는 의 행들의 선형결합이다. 벡터-행렬 곱셈의 선형결합 정의에 의하면 다음을 만족하는 벡터 가 있다.
따라서 가 의 행들의 선형결합으로 표현될 수 있음을 보여준다.
Corollary : 행렬 와 에 대해, 만약 이 가역적이면 Row Row 이다.
proof : 을 가지고 위의 Lemma 에 적용하면, Row Row 를 얻는다. 라고 하면, 은 가역적이므로, 역행렬 가 존재한다. 을 가지고 위의 Lemma 에 적용하면 Row Row 를 얻는다. 이므로, Row Row 이 증명된다.
Example 8.1.5 : 다음의 예를 보자.
라고 하면, 이다. 위의 Lemma 를 이용하여 Row Row 이고 Row Row 임을 보여준다. Row 에 속하는 모든 벡터 는 다음과 같이 표현될 수 있다.
위의 식에서 가 벡터와 행렬 의 곱셈으로 표현될 수 있음을 보여준다. 또한, 가 Row 임을 보여준다. Row 내의 모든 벡터는 Row 에 속하므로, Row Row 이다. 이번에는 Row Row 임을 보여야 한다. 이므로, Row Row 임을 보여 주면된다. Row 에 속하는 모든 벡터 는 다음과 같이 표현될 수 있다.
위의 식은 가 벡터와 행렬 의 곱셈으로 표현될 수 있음을 보여준다. 또한, 가 Row 에 속한다는 것을 보여준다.
8.1.7 - 8.1.9 생략
8.2 생략
8.3 다른 문제에 대해 가우스 소거법 사용하기
앞에서 사다리꼴 행렬에서 영이 아닌 원소를 가지는 행들은 그 행렬의 행공간에 대한 기저를 형성한다는 것을 살펴보았다. 또한, 가우스 소거법을 사용하여 행공간을 변경하지 않고 행렬을 사다리꼴로 어떻게 변환하는지 살펴보았다. 이것을 이용하면 행렬의 행공간에 대한 기저를 찾는 알고리즘을 얻을 수 있다. <br />또한, 가우스 소거법은 아래의 문제들을 해결하는 데도 사용할 수 있다.
선형시스템의 해 구하기
영공간에 대한 기저 찾기
8.3.1 가역행렬 과 사다리꼴의 행렬
가우스 소거법을 위의 문제들을 해결하는 데 사용하는 핵심은 8.1.5에서 보았듯이, 입력 행렬을 사다리꼴 행렬로 만드는 데 사용되는 기본행-덧셈 연산을 찾는 것이다. 8.1.5의 기본행-덧셈 연산은 행렬에 적용될 수 있는데, 이것은 기본행-덧셈 행렬 을 그 행렬과 곱합으로써 이루어 진다. 행렬 를 가지고 시작해보자.
하나의 행-덧셈 연산을 수행하여 행렬 를 얻는다.
그 다음에, 또 다른 행-덧셈 연산을 이 행렬에 대해 수행하여 행렬 를 얻는다.
이런 방식으로 계속 진행하면, 만약 가 행-덧셈 연산의 총 개수일 경우 마지막으로 얻어지는 행렬은 아래와 같다.
을 에서 까지의 곱이라 하면, 가우스 소거법을 에 적용한 최종 결과인 행렬은 이다.
Proposition : 임의의 행렬 에 대해, 는 사다리꼴 행렬인 가역행렬 이 있다.
8.3.2 행렬 곱셈없이 계산하기
Example 8.3.2 : 다음 예제를 통해 을 계산해 보자.
처음에는 을 아래와 같이 단위행렬로 정의한다.
첫 번째 행-덧셈 연산은 네 번째 행에서 두 번째 행의 2배를 뺀다. 이것을 행렬-행렬 곱셈으로 나타내면 아래와 같다.
다음 행-덧셈 연산은 두 번째 행의 3배를 다섯 번째 행에서 빼는 것이다.
마지막 행-덧셈 연산은 네 번째 행의 배를 다섯 번째 행에서 빼는 것이다.
그럼, 실제로 위의 식이 맞는 식인지 파이썬의 numpy 모듈을 이용하여 계산해 보자.
import numpy as np
M = np.matrix([
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, -2, 0, 1, 0],
[0, -5/3, 0, -2/3, 1]
])
A = np.matrix([
[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[1, 2, 3, 4, 5],
[0, 0, 0, 6, 7],
[0, 0, 0, 9, 8]
])
print(np.matmul(M, A))
'''
[[ 0. 2. 3. 4. 5.]
[ 0. 0. 0. 3. 2.]
[ 1. 2. 3. 4. 5.]
[ 0. 0. 0. 0. 3.]
[ 0. 0. 0. 0. 0.]]
'''
이번에는, 8.1.4의 row_reduce() 함수를 이용하여 행렬 을 계산하는 코드를 작성해보자. 아래의 코드는 행렬 과 를 구한 뒤 두 행렬을 사다리꼴(echelon form)으로 변환해준 결과를 반환한다.
def row_reduce(mat):
rref = []
M_e = []
row_idx = list(range(len(mat)))
col_idx = len(mat[0])
# mat과 크기가 같은 단위행렬 생성
M = [[0 for c in range(len(mat))] for r in range(len(mat))]
for i in range(len(M)):
M[i][i] = 1
for c in range(col_idx):
rows_with_nonzero = [r for r in row_idx if mat[r][c] != 0]
if rows_with_nonzero:
pivot = rows_with_nonzero[0]
row_idx.remove(pivot)
rref.append(mat[pivot])
M_e.append(M[pivot])
for r in rows_with_nonzero[1:]:
if r is not pivot:
multiplier = mat[r][c] / mat[pivot][c]
mat[r] = [a - multiplier*b for a, b in zip(mat[r], mat[pivot])]
M[r] = [a - multiplier*b for a, b in zip(M[r], M[pivot])]
for r in row_idx:
rref.append(mat[r])
M_e.append(M[r])
return rref, M_e
>>> mat = [[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[1, 2, 3, 4, 5],
[0, 0, 0, 6, 7],
[0, 0, 0, 9, 8]]
>>> rref, M = row_reduce(mat)
>>> rref
[[1, 2, 3, 4, 5],
[0, 2, 3, 4, 5],
[0, 0, 0, 3, 2],
[0.0, 0.0, 0.0, 0.0, 3.0],
[0.0, 0.0, 0.0, 0.0, 0.0]]
>>> M
[[0, 0, 1, 0, 0],
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0.0, -2.0, 0.0, 1.0, 0.0],
[0.0, -1.6666666666666667, 0.0, -0.6666666666666666, 1.0]]8.4 가우스 소거법을 사용하여 행렬-벡터 방정식 풀기
행렬-벡터 방정식의 해를 구한다고 해보자.
가 사다리꼴 행렬 가 되는 행렬 을 계산해보자. 양변에 을 곱하면 아래와 같다.
를 바로 위의 식에 대한 해라고 하면, 이고, 양변에 을 곱하면 이다. 즉, 이므로 는 원래 방정식의 해라는 것을 알 수 있다.
'Linear Algebra > Coding the Matrix' 카테고리의 다른 글
| [코딩더매트릭스]Chap10 - 직교화 Orthogonalization (1) | 2018.06.11 |
|---|---|
| [코딩더매트릭스]Chap09 - 내적 Inner Product (0) | 2018.05.17 |
| [코딩더매트릭스]Chap07 - 차원 Dimension (0) | 2018.05.02 |
| [코딩더매트릭스]Chap06 - 기저 Basis (0) | 2018.04.19 |
| [코딩더매트릭스]Chap05 - 행렬 The Matrix (2) | 2018.03.14 |