| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 코딩더매트릭스
- 딥러닝
- hive
- NumPy
- Java
- tensorflow
- 파이썬
- effective python
- 알고리즘
- HelloWorld
- 선형대수
- 그래프이론
- yarn
- C
- RNN
- hadoop2
- C언어
- 하이브
- 하둡2
- LSTM
- 텐서플로
- scrapy
- codingthematrix
- recursion
- Sort
- GRU
- 주식분석
- collections
- graph
- python
- Today
- Total
EXCELSIOR
[코딩더매트릭스]Chap07 - 차원 Dimension 본문
차원 - Dimension
7.1 기저의 크기
7.1.1 Morphing 보조 정리와 그 응용
Lemma (Morphing Lemma) : 는 벡터공간이라고 하자. 는 에 대한 생성자들의 집합이라 하고, 는 에 속하는 벡터들로 구성된 선형독립인 집합(즉, 기저)이라고 하면, 이다. <br />
Theorem (Basis Theorem) : 는 벡터공간이라 하고, 에 대한 모든 기저(basis)는 동일한 크기를 가진다.
Proof : 과 는 에 대한 두 기저라고 하자. 과 를 위의 Morphing Lemma 에 적용하면 라고 할 수 있다. 와 을 적용하면 이다. 이 둘의 부등식을 결합하면 를 얻을 수 있다.
Theorem : 는 벡터공간이라고 하면, 에 대한 생성자들의 집합이 에 대한 생성자들로 구성된 가장 작은 집합 이 되는 필요충분 조건은 이 집합이 에 대한 기저인 것이다.
Proof : 는 에 대한 생성자들의 집합이라고 하자. 그렇다면, 증명해야 하는 것은
(1) 만약 가 에 대한 기저이면 는 에 대한 생성자들로 구성된 가장 작은 집합이다.
(2) 만약 가 에 대한 기저가 아니면 생성자들로 구성된 보다 더 작은 집합이 존재한다.
를 기저라고 하고, 는 에 대한 생성자들로 구성된 가장 작은 집합이라고 하자. 위의 Morphing Lemma 에 의하면, 이고, 따라서 또한 생성자들의 가장 작은 집합이다.
는 기저가 아니라고 해보자. 기저는 생성자들로 구성된 선형독립 인 집합이다. 그러므로 는 기저가 아니라 했으니, 는 생성자들로 구성된 선형종속인 집합이다. 6.5.4의 Lemma에 따르면 내에 다른 벡터들의 생성에 속하는 일부 벡터들이 있다. 그러므로 Superfluous-Vector Lemma 에 의해, 에서 제거하면 에 대한 생성자들의 집합이 되는 일부 벡터가 존재한다. 따라서 는 생성자들로 구성된 가장 작은 집합이 아니다.
7.1.2 생략
7.2 차원과 랭크 - Dimension and Rank
7.2.1 정의 및 예제
Definition : 벡터공간의 차원 은 그 벡터공간에 대한 기저의 크기로 정의한다. 벡터공간 의 차원은 로 표현한다. <br />
Example 7.2.2 : 에 대한 하나의 기저는 표준 기저 이다. 그러므로 의 차원은 기저의 크기인 3, 즉 이다.
Example 7.2.3 : 좀 더 일반적으로, 임의의 필드 와 유한집합 에 대해, 에 대한 하나의 기저는 표준기저이고 이것은 벡터들로 구성되므로, 의 차원은 이다.
<br />
Definition : 벡터들의 집합 의 랭크(rank)를 Span 의 차원이라 정의한다. 의 랭크는 rank 로 나타낸다.
Example 7.2.6 : 벡터 은 선형종속이다. 그러므로 이 벡터들의 랭크는 보다 작다. 이들 중 임의의 두 벡터는 세 벡터들의 Span에 대한 기저를 형성한다. 따라서 랭크는 이다.
<br />
Proposition : 벡터들로 구성된 임의의 집합 에 대해, rank <br />
Definition : 행렬 에 대해, 의 행랭크 는 그 행렬의 행의 랭크이고, 의 열랭크 는 그 행렬의 열의 랭크이다. 즉, 의 행랭크는 Row 의 차원이고, 의 열랭크는 Col 의 차원이다.
Example 7.2.10 :
이 행렬의 행벡터는 이고, 위의 Example 7.2.6 에서 살펴보았듯이 행벡터의 랭크는 이므로, 의 행랭크는 이다.
행렬 의 열벡터는 이다. 세 번째 벡터는 영벡터이므로, 열공간을 생성하는 데 필요하지 않다. 나머지 두 벡터는 선형독립이므로 열랭크는 이다.
<br />
Example 7.2.11 :
행벡터 들은 선형독립이므로 의 행랭크는 이다.
의 열벡터 들은 처음 세 열은 선형독립이고 은 앞의 세 벡터의 선형결합으로 나타낼 수 있으므로 열랭크는 이다.
<br />
위의 두 예제를 통해 행랭크와 열랭크가 동일하다는 것을 알 수 있다. 이것은 우연히 동일한 것이 아니라, 어떤 행렬에 대해서도 행랭크 와 열랭크 가 동일 하다.
7.2.2 기하학적 구조
좌표계에 대해 기하학적으로 이해 해보자. 기하적 객체의 차원은 객체의 점들에 할당되어야 하는 최소 개수의 좌표이다. 좌표의 수는 기저의 크기이고, 기저의 크기는 주어진 벡터들로 구성된 집합의 랭크이다.
Span 은 직선, 즉 1차원 객체이다. Span 은 점, 즉 1차원 구조이다. 첫 번째 벡터공간은 차원이 이고 두 번째 벡터공간은 차원이 이다.
Span 은 의 모든 것, 즉 2차원 객체를 구성한다. 반면, Span 은 직선, 즉 1차원 객체이다.
Span 은 의 모든 것, 즉 3차원 객체이다. 반면에, Span 은 평면 즉, 2차원 객체이다.
<br />
7.2.3 생략
7.2.4 상의 벡터공간의 크기
는 상의 벡터공간 에 대한 차원이라 하고, 는 에 대한 기저라고 하면, 6.7.1의 Unique Representation Lemma에 의해, 내의 각 벡터는 기저벡터들의 선형결합으로 유일하게 표현된다. 따라서, 내 벡터들의 수는 이 기저벡터들의 선형결합들의 수와 동일하다. 개의 기저벡터가 있으므로, 각 선형결합에는 개의 계수가 있다. 각 계수는 또는 이므로 개의 다른 선형결합이 있다.
7.2.5 에 속하는 벡터들의 임의의 선형독립 집합은 에 대한 기저를 형성하도록 확장될 수 있다.
Lemma (Superset-Basis Lemma) : 임의의 벡터공간 와 벡터들로 구성된 임의의 선형독립 집합 에 대해, 는 의 모든 원소를 포함하는 기저를 가진다.
Proof : 6.3.1 에서 보았던 Grow 알고리즘을 사용해보자.
7.2.6 차원 원리(Dimension principle)
Lemma (Dimension Principle) : 만약 가 의 부분공간(subspace)이면, 다음 성질이 성립한다.
Property D1 : 이다.
Property D2 : 만약 이면 이다.
proof : 는 에 대한 기저라고 하면, 7.2.5의 Superset-Basis Lemma에 의해 를 포함하는 에 대한 기저 가 있고, 의 크기는 적어도 이다. 이 의미는 Property D1을 증명한다. 만약 의 크기가 정확히 이면 는 이외의 다른 벡터는 포함하지 않으며, 의 기저는 의 기저임을 보여주어 Property D2를 증명한다.
Example 7.2.15 : 라고 해보자. 는 의 부분공간이다. 집합 은 선형독립이고, 따라서 이다. 이므로 Property D2는 임을 보여준다.
Example 7.2.16 : 집합에 대해 이므로, Span 이다. 내의 모든 벡터는 -벡터이므로, Span 는 의 부분공간이고, Span 이다.
위의 예제를 통해 다음을 알 수 있다.
Proposition : -벡터들로 구성된 임의의 집합의 랭크는 보다 작거나 같다.
7.2.7 생략
7.2.8 Rank 정리
앞의 예제에서 살표보았듯이 행랭크와 열랭크는 동일하다. 이제 왜 행랭크와 열랭크가 같은지 알아보자. <br />
Theorem (Rank Theorem) : 임의의 어떠한 행렬에 대해, 행랭크와 열랭크는 동일하다.
Proof : 임의의 행렬 에 대해 행랭크는 의 열랭크보다 작거나 같다. 동일한 주장을 에 적용하면 의 행랭크는 의 열랭크보다 작거나 같다. 즉, 의 열랭크는 의 행랭크보다 작거나 같다. 이 두 부등식을 결합하면 의 행랭크는 의 열랭크와 동일하다. <br />는 행렬이라 하자. 행렬 를 열벡터로 나타내 보자:
은 의 열랭크라 하고 은 의 열공간에 대한 기저라 하자. <br /> 의 각 열 에 대해 는 의 에 대한 좌표 표현이라 하자. 그러면, 행렬-벡터 곱셈의 선형결합 정의에 의해 다음과 같이 표현된다.
행렬-행렬 곱셈의 행렬-벡터 정의에 의하면, 다음과 같이 표현되며,
이것을 다음 처럼 쓸 수 있다.
는 개의 열을 가지며 는 개의 행을 가진다. <br />이제, 와 를 열 대신에 행들로 구성된 행렬로 생각해 보자.
행렬-행렬 곱셈의 벡터-행렬 정의에 의하면, 의 행 인 는 의 행 인 를 행렬 에 곱한 것이다.
그러므로, 벡터-행렬 곱셈의 선형결합에 의하면 의 모든 행은 의 행들의 선형결합이다. 따라서, 의 행공간은 의 행공간의 부분공간이다. 의 행공간의 차원은 , 즉 의 행의 수보다 작거나 같다. 따라서, 의 행랭크는 보다 작거나 같다. <br />위에서 보았듯이, 임의의 행렬 에 대해 의 행랭크는 의 열랭크보다 작거나 같다. 임의의 행렬 에 대해, 이결과를 에 적용하면 다음이 성립한다.
이 결과를 에 적용하면,
따라서, 의 행랭크는 의 열랭크와 동일하다.
Definition : 행렬의 랭크 는 그 행렬의 열랭크와 동일하고, 이것은 또한 그 행렬의 행랭크와 같다.
7.3 직합 - Direct Sum
7.3.1 정의
와 는 필드 상의 -벡터들로 구성된 두 개의 벡터공간이라고 하자.
Definition : 만약 와 가 오로지 영벡터만을 공유한다면 와 의 직합 (direct sum)은 아래와 같이 정의하며,
로 나타낸다. 즉, 는 의 벡터와 의 벡터의 모든 합으로 구성된 집합이다.
Example 7.3.3 : Span 라 하고, 는 의 영공간(null space) 이라 하자. 와 는 아래의 이유로, 가 성립하지 않는다.
벡터 는 이므로 내에 있다.
벡터 는 아래와 같이 내에 있다.
Example 7.3.4 : Span , Span 라고 하자. 와 각각은 단일 벡터의 Span이고, 따라서 직선을 형성한다. <br />유일한 교점은 원점(0,0,0)이다. 따라서, 는 성립한다. 이 직합은 Span 이며 두개의 직선을 포함하는 평면이다.
Proposition : 직합(direct sum) 는 벡터공간이다.
7.3.2 직합에 대한 생성자
바로 위의 Example 7.3.4 에서, 에 대한 생성자들의 집합과 에 대한 생성자들의 집합의 합집합을 구하면 직합 에 대한 하나의 생성자 집합이 얻어진다. <br />
Lemma : 아래 집합의 합집합은
의 생성자들의 집합
의 생성자들의 집합
에 대한 생성자들의 집합이다.
proof : Span , Span 라고 하면,
내의 모든 벡터는 으로 표현할 수 있다.
내의 모든 벡터는 으로 표현할 수 있다.
따라서, 내의 모든 벡터는 다음과 같이 나타낼 수 있다.
7.3.3 직합에 대한 기저
Lemma (Direct Sum Basis Lemma) : 의 기저와 의 기저의 합집합은 의 기저이다.
Proof : 은 에 대한 기저라 하고, 은 에 대한 기저라고 하면, 기저는 생성자들의 집합이므로, 은 에 대한 생성자들의 집합이다. 이제 기저라는 것을 보이기 위해서 선형독립 이라는 것을 보여주면 된다. 다음 식을 가정해보자.
위의 식은 다음이 성립한다.
좌변은 내의 벡터이고, 우변은 내의 벡터이다. 의 정의에 의하면, 와 둘 모두에 있는 유일한 벡터는 영벡터이다. 이것은 다음을 보여준다.
위의 식들은 선형독립에 의해 자명하다(trivial).
위의 Lemma(Direct Sum Basis Lemma) 에 의해 다음과 같은 Corollary가 가능하다.
Corollary (Direct-Sum Dimension Corollary) :
위의 Corollary(따름정리)는 Kernel-Image Theorem을 증명하는데 사용할 것 이다.
7.3.4 벡터의 고유분해 - Unique Decomposition
Corollary (Direct-Sum Unique Representation Collorary) : 내의 임의의 벡터는 로 유일하게 표현된다. (단, )
Proof : 은 에 대한 기저라 하고, 은 에 대한 기저라고 하면, 은 에 대한 기저이다. 는 내의 임의의 벡터라고 하자. 는 다음과 같이 표현된다.
를 로서 나타내는 방법을 고려해보자. 는 내에 있고, 는 내에 있다. 를 의 기저에 대해 나타내고, 를 의 기저에 대해 표현하면 다음과 같다.
Unique-Representation Lemma 에 의해 이므로, 는 내의 벡터와 내의 벡터의 합으로 유일하게 명시된다.
7.3.5 여부분공간 - Complementary subspace
Definition : 만약 이면, 와 는 의 여부분공간(complementary subspace, complementary: 상호보완적인) 이라 한다.
<br />
Proposition : 임의의 벡터공간 와 의 임의의 부분공간 에 대해, 을 만족하는 의 부분공간 가 있다.
Proof : 는 에 대한 기저라고 하자. 7.2.5의 Superset-Basis Lemma에 의하면, 를 포함하는 에 대한 기저가 있다. 이 기저를 로 나타내고, Span 이라고 하자. 내의 임의의 벡터 는 이 기저에 대해 다음과 같이 좌표표현으로 나타낼 수 있다.
따라서, 만약 직합(direct-sum)이 옳다는 것을 보여 줄 수 있으면, 즉 와 둘 모두에 속하는 유일한 벡터는 영벡터라는 것을 보여줄 수 있으면 임을 보여주는 것이다.
어떤 벡터 가 와 둘 모두에 속한다고 하면 아래와 같이 쓸 수 있다.
이것이 의미하는 것은 이며, 는 영벡터임을 보여준다.
7.4 차원과 선형함수
선형함수가 가역적인지 아닌지 판단할 수 있는 기준에 대해 알아 보도록 하자. 이것은 또한 행렬이 가역적인지 판단한느 기준을 제공해 준다. 또한 이러한 기준은 중요한 정리인 Kernel-Image 정리를 기반으로 한다.
7.4.1 선형함수의 가역성
선형함수 가 가역적인지 어떻게 판단할 수 있을까? 알아야 하는 것은 5장에서 배웠던 가 단사(one-to-one)인지 전사(onto)인지의 여부이다. <br />
One-to-One Lemma에 의하면, 가 단사함수일 필요충분조건은 그 커널(kernel)은 자명한 경우 즉, 인 경우이다. <br/>
5.10.6에서 의 상은 Im 이다. 따라서, 가 전사함수일 필요충분조건은 Im 인 경우이다. <br />
Im 가 의 부분공간임을 보여줄 수 있다. 7.2.6의 Dimension principle Lemma에 의하면 가 전사함수일 필요충분 조건은 Im 이다.
선형함수 가 이고 Im 이면 가역적(Invertible)이다.
7.4.2 가장 큰 가역적인 서브함수(Subfunction)
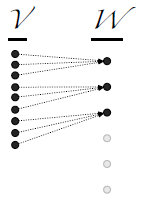
는 아래의 그림과 같이 비가역적 선형함수라고 하자.
그렇다면 여기서 가역적인 서브함수 를 정의해보자. 여기서 서브함수 란 는 의 부분집합이고 는 의 부분집합이며 는 의 모든 원소에 대해 와 동일하다는 것을 의미한다. <br />
먼저, 가 전사함수가 되도록 를 아래의 그림처럼 선택한다. 그리고, 은 에 대한 기저라고 하자.
그런다음, 은 의 원상(pre-image)라고 하자. 즉, 을 만족하는 내의 임의의 벡터들 을 아래의 그림처럼 선택하고, 는 Span 라고 정의하자.
마지막으로 는 라고 정의한다. <br />
Lemma : 는 전사함수이다.
proof : 는 공역 내의 임의의 벡터라고 하고, 다음을 만족하는 스칼라 이 있다.
는 선형이므로,
따라서, 는 의 상이다.
<br />
Lemma : 는 단사함수이다.
Proof : One-to-One Lemma에 의해, 의 커널(kernel)이 자명한, 즉 임을 보여준면 된다. 는 내에 있고 라고 해보자. Span 이므로, 다음을 만족하는 스칼라 이 존재한다.
양변에 를 적용하면 다음과 같다.
은 선형독립이므로, 이고, 이다.
<br />
Lemma : 은 에 대한 기저를 형성한다.
Proof : 는 의 생성이라고 정의되었기 때문에, 이 벡터들이 선형독립이라는 것만 보여주면 된다. 아래의 식을 가정해 보자.
양변에 를 적용하면 다음을 얻는다.
은 선형독립이므로, 이다.
<br />
Example 7.4.4 : 이라 하고, 은 라고 정의하자. Col Span 이라고 정의하자. 에 대한 하나의 기저는 , 이다. <br />
이제, 과 에 대한 원상(pre-image)를 선택하자. 에 대해 계산된 원상은 아래와 같다.
Span 라고 하면, 에 의해 정의된 함수 은 전단사함수이다.
7.4.3 Kernel-Image 정리
함수 에서 가역 서브함수 를 구성하는 것은 서브함수의 정의역을 원래 선형함수 의 커널에 연관시킨다.<br />
Lemma :
Proof : 다음 두 가지 항목을 증명해야 한다.
와 는 영벡터만을 공유한다.
내의 모든 벡터는 내의 벡터와 내의 벡터의 합이다.
이미 위의 7.4.2 에서 의 커널은 자명하다는 것을 보여주었다. 따라서, 에 속하는 의 유일한 벡터는 영(0)이고, 이를 통해 '와 는 영벡터만을 공유한다.' 는 증명이 된다.
는 내의 임의의 벡터이고, 라고 하자. 는 전사함수이므로, 그 정의역인 는 를 만족하는 벡터 를 포함한다. 그러므로, 이고, 따라서 이 성립한다. 따라서, 는 내에 있고, 이다.
Example 7.4.6 : Example 7.4.4에서 이라 하고, 은 라고 정의하자. 에 대한 기저는 위의 Example 7.4.4에서 로 구성된다. 의 커널은 Span 이다. 그러므로 (Span ) (Span ) 이다.
Theorem (Kernel-Image Theorem) : 임의의 선형함수 에 대해,
Proof : 임을 보여준다. 7.3.3의 Direct-Sum Dmension Corollary에 의하면,
은 에 대한 기저를 형성하고, 이러한 벡터들의 수 은 에대한 기저의 크기와 동일하다.
7.4.4 선형함수의 가역성 - 다시보기
위의 Kernel-Image Theorem을 이용해 선형함수의 가역성을 판단하는 데 좀 더 나은 기준을 제시할 수 있다.
Theorem (Linear-Function Invertibility Theorem) : 는 선형함수라고 하자. 그러면, 가 가역적일 필요충분조건은 이고, 이다.
7.4.5 Rank-Nullity 정리
행렬 에 대해, 을 라고 하자. 위의 Kernel-Image Theorem에 의해, 이다. 의 커널은 의 영공간(Null Space)이고, 행렬-벡터 곱셈의 선형결합 정의에 의해 의 상은 의 열공간이고, 따라서 다음을 얻는다.
의 차원은 , 즉 의 열의 개수이고, 의 열공간의 차원은 의 랭크라고 한다. 행렬 의 영공간의 차원은 의 Nullity 라고한다. <br />
Theorem (Rank-Nullity Theorem) : 임의의 -열 행렬 에 대해,
7.4.6 생략
7.4.7 행렬의 가역성
Corollary : 는 행렬이라고 하면, 가 가역적이 될 필요충분조건은 이고, 의 열들은 선형독립일 때다.
Proof : 는 필드라고 하고, 은 라 하면, 가 가역행렬이 될 필요충분조건은 가 가역함수인 것이다. 7.4.4의 Theorem에 의하면, 가 가역적일 필요충분조건은 이고 이다. 즉, 이고, 이다. 또한, 일 필요충분조건은 행렬의 열벡터들이 선형결합인 것이다.
Corollary : 가역행렬의 전치행렬은 가역적이다.
Proof : 는 가역행렬이라고 하면, 는 정방행렬이고 그 열들은 선형독립이다. 은 열들의 개수라고 하고, 행렬을 다음과 같이 표현하자.
의 열들은 선형독립이므로, 의 랭크는 이다. 는 정방행렬이므로, 개의 행을 가진다. 의 행랭크는 이고, 그 행들은 선형독립이다. 전치행렬 또한 마찬가지다.
Corollary : 와 는 정방행렬이고 는 단위행렬이라고 하면, 와 는 서로의 역행렬이다.
Proof : 는 행렬이라 하고, 는 행렬이라고 하면, 는 단위행렬 이다. 의 열들은 선형독립이라는 것을 보여주자. 는 을 만족하는 임의의 벡터라고 하면, 이고, 이므로, 이다. 는 가역적이므로 의 역행렬을 로 나타내고 은 단위행렬 이다.
Example 7.4.15 : 은 정방행렬이지만 열벡터들이 선형독립이 아닌 선형종속이므로 이 행렬은 가역적이지 않다.
7.4.8 행렬의 가역성과 기저 변경
동일한 공간의 기저 과 에 대해, 행렬 가 존재하며, 이 행렬 를 곱하면 에 대한 어떤 벡터의 좌표 표현이 동일한 벡터의 에 대한 좌표표현으로 변환된다. 행렬 는 가역적이다. 두 기저는 동일한 크기를 가져야 하며, 따라서 는 정방행렬이다.
'Linear Algebra > Coding the Matrix' 카테고리의 다른 글
| [코딩더매트릭스]Chap09 - 내적 Inner Product (0) | 2018.05.17 |
|---|---|
| [코딩더매트릭스]Chap08 - 가우스 소거법 Gaussian Elimination (0) | 2018.05.04 |
| [코딩더매트릭스]Chap06 - 기저 Basis (0) | 2018.04.19 |
| [코딩더매트릭스]Chap05 - 행렬 The Matrix (2) | 2018.03.14 |
| [코딩더매트릭스]Chap04 - 벡터공간 Vector Space (0) | 2018.02.27 |