| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- codingthematrix
- scrapy
- HelloWorld
- 파이썬
- NumPy
- 하둡2
- 하이브
- 주식분석
- python
- graph
- 선형대수
- 코딩더매트릭스
- 그래프이론
- hadoop2
- C
- C언어
- effective python
- hive
- 텐서플로
- recursion
- yarn
- Sort
- 딥러닝
- Java
- LSTM
- tensorflow
- collections
- RNN
- 알고리즘
- GRU
- Today
- Total
EXCELSIOR
[코딩더매트릭스]Chap10 - 직교화 Orthogonalization 본문
[코딩더매트릭스]Chap10 - 직교화 Orthogonalization
Excelsior-JH 2018. 6. 11. 08:22직교화(Orthogonalization)
이번 장의 첫 번째 목적은 다음 문제에 대한 알고리즘을 제시하는 것이다.
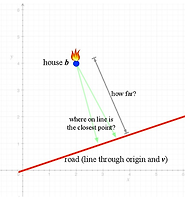
Computational Problem : (여러 벡터들의 Span 내에 있는 가장 가까운점 ) 주어진 벡터 와 실수 벡터들 에 대해, Span 내에 있으며 에서 가장 가까운 벡터를 찾아보자.
라 하고, 행렬-벡터 곱셈의 선형결합 정의에 의하면, Span 내 벡터들의 집합은 로 표현할 수 있는 벡터들의 집합이다. 따라서, 결국 계수(좌표)들을 찾는 것은 을 최소화 하는 벡터 를 찾는 것과 같다. 이것을 최소제곱 (least-squares) 문제라고 한다.
10.1 복수의 벡터들에 직교하는 투영
9장에서 살펴보았던 소방차 문제 와 같이 직교성과 투영(projection)을 사용하여 풀 수 있다.
10.1.1 벡터들의 집합에 대한 직교
9장에서는 한 벡터가 다른 벡터에 직교한다는 것이 무엇을 의미하는지 살펴 보았다면, 이번 장에서는 한 벡터가 벡터들의 집합에 직교하는 것이 무엇을 의미하는지를 살펴본다.
Definition : 벡터 는 만약 내의 모든 벡터에 직교하면 벡터들의 집합 에 직교한다.
Example 10.1.2 : 벡터 은 과 에 직교하므로 집합 에 직교한다. 또한, 벡터는 무한 집합 Span 에 직교한다. 그 이유는 내의 모든 벡터는 이고 다음이 성립하기 때문이다.
Lemma : 벡터 가 벡터들 각각에 직교할 필요충분조건은 가 Span 내의 모든 벡터에 직교하는 것이다.
Proof : 는 에 직교한다고 하고, 는 Span 내의 임의의 벡터라고 하자. 는 에 직교한다는 것을 보이면 된다. Span의 정의에 의하면 다음을 만족하는 계수 이 있다.
그러므로, 직교의 성질을 사용하면 다음이 성립한다.
따라서, 는 에 직교한다. 이제, 는 Span 의 모든 벡터에 직교한다고 해보자. Span 은 을 포함하므로 는 에 직교한다.
10.1.2 벡터공간상으로의 투영 및 벡터공간에 직교하는 투영
Definition : 벡터 와 벡터공간 에 대해, 의 상으로의 투영 () 과 의 에 직교하는 투영 () 을 정의해 보자. 그러면, 다음과 같이 쓸 수 있다.

그리고, 는 에 속하고, 는 에 속하는 모든 벡터에 직교한다.
Lemma : 는 벡터공간이라 하고, 는 벡터라고 하자. 에 속하며 에 가장 가까운 점은 이고, 그 거리는 이다.

Proof : 와 사이의 거리는 이다. 는 의 임의의 점이라고 하면, 는 보다 에 가깝지 않다는 것을 보여 보자.
우변에서 이고, 는 에 속하는 두 벡터의 차이이므로 내에 있다. 는 에 직교하므로, 피타고라스 정리에 의하면 다음이 성립한다.
따라서, 이면 이 성립한다.
10.1.3 벡터들의 리스트에 직교하는 투영 - 첫 번째 시도
파이썬을 이용해서 다음을 만족하는 project_orthogonal() 함수를 작성해보자.
input : 벡터 , 벡터들의 리스트
output : Span 에 직교하는 의 투영 (즉, )
아래의 코드는 9.3.4 에서 작성한 project_along() 함수를 이용하여 project_orthogonal() 함수를 구현한 코드이다.
위의 project_orthogonal() 함수는 문제가 있다. 예를 들어 , 라고 할 경우 project_orthogonal() 의 출력값은 [-0.5, 0.5] 이다. 이 벡터는 아래의 그림과 같이 의 과 직교하지 않는다.

10.2 서로 직교 하는 벡터들의 리스트에 직교하는 의 투영
그렇다면, 위의 project_orthogonal() 함수가 동작하도록 하는 들을 만들어 보자. 예를 들어, 에 , 과 라고 하면 다음과 같은 결과가 나온다.
이 결과값은 의 과 두 벡터에 각각 직교한다. 또한 과 는 서로 직교한다. 이것을 9.3.4 에서 배웠던 공식을 이용하면 다음과 같다.
이고, 이므로,
즉, 10.1.3과 달리 input 값을 아래와 같이 설정해주면 project_orthogonal()은 제대로 동작한다.
input : 벡터 , 서로 직교 하는 벡터들의 리스트
output : 에 속하는 벡터들에 직교하는 의 투영
10.2.1 프로시저 project_orthogonal()이 맞게 동작하는지 증명하기
Theorem (project_orthogonal()의 정확성) : 벡터 와 서로 직교하는 벡터들의 리스트 vlist 에 대해, 함수 project_orthogonal(b, vlist) 는 을 반환한다. 이때, 은 vlist 에 속하는 벡터들에 직교하며 은 vlist 에 속하는 벡터들의 Span에 속한다.
함수 project_orthogonal()이 맞다는 것을 증명하기 위해, 이터레이션 후 를 포함하는 vlist가 에 대해 참이라는 것을 보여 준다. 이러한 방법을 루프불변 (loop invariant)
Lemma (project_orthogonal에 대한 루프불변) : len(vlist) 라고 하면, 에 대해, 는 이터레이션 후 변수 b(project_orthogonal의 결과값, 즉 ) 의 값이라고 하자.
는
vlist에 속하는 첫 개 벡터들에 직교한다. 은
vlist에 속하는 첫 개 벡터들의 Span에 속한다.
project_orthogonal함수에 의해 반환되는 벡터 은 모든 이터레이션 후 의 값이며 로 나타낸다. 루프불변의 에 를 대입하면 다음을 얻는다.
은
vlist의 첫 개 벡터에 직교하고 는 Span {vlist}에 속한다.Proof : 증명은 에 대해 귀납법을 사용한다. 인 경우, 루프불변은 참이다: 는 첫 0개 벡터들의 각각에 직교하고, 은 첫 0개 벡터들의 Span에 속한다(왜냐하면, 영벡터이기 때문에!). 이터레이션에 대해 루프불변이 성립한다고 가정하자. 그런 다음 -이터레이션에 대해 루프불변이 성립함을 증명하면 된다.
vlist를 로 나타내자. 번째 이터레이션에서 함수는 다음을 계산한다.
여기서 이다. 귀납 가설은 이 첫 개 벡터들에 직교하는 의 투영이라는 것이다.
가 에 속하는 각 벡터에 직교한다는 것을 증명해야 한다. 라고 하면
또한, 는
vlist의 첫 개의 벡터들의 Span에 속한다는 것을 증명해야 한다. 귀납가설에 의하면, 은 개 벡터들의 Span에 속한다.
10.2.2 project_orthogonal() 보완하기
이 벡터들 의 생성에 속한다는 것을 다음과 같이 표현할 수 있다.
위의 식을 반영하여, project_orthogonal(b, vlist) 를 보완한 aug_project_orthogonal(b, vlist) 함수를 구현해보자.
input : 벡터 b, 서로 직교하는 실수 벡터들의 리스트 [
output: 튜플 () 이 튜플은 다음을 만족한다.
튜플의 첫 번째 원소는 의 투영 이며 이것은 Span 에 직교한다.
튜플의 두 번째 원소는 딕셔너리 이며 다음을 만족한다.
10.3 생성자들의 직교집합 만들기
이번 장의 목표는 맨처음에서도 살펴 보았듯이 임의의 벡터들 으로 구성된 집합의 생성에 직교하게 를 투영하는 것이다. 10.1 ~ 10.2 까지 구현했던 함수들은 서로 직교하는 벡터들로 구성된 에 직교하는 를 투영하는 것에서는 제대로 동작하였다.
이제는 서로 직교하지 않을 수도 있는 벡터들 의 생성에 직교하게 를 투영해보자. 이를 위해서는 Span 에 대한 서로 직교하는 생성자(generator) 를 먼저 찾아야 한다.
따라서, 새로운 함수인 직교화(orthogonalization) 가 필요하다.
input : 실수 벡터들의 리스트
output : 다음을 만족하는 서로 직교하는 벡터들 의 리스트
10.3.1 orthogonalize() 프로시저
orthogonalize() 함수를 구현하기 위해 위에서 작성한 project_orthogonal() 함수를 반복하여 서로 직교하는 벡터들의 리스트를 만들어 준다.
먼저, 벡터를 고려해 보자. 집합 은 서로 직교하는 벡터들의 집합이므로 이라고 정의하자. 다음으로, 는 에 직교하는 의 투영이라고 정의하자. 그렇게 되면, 은 서로 직교하는 벡터들의 집합이다. 그 다음으로 는 의 투영이고 과 직교하는 벡터라고 하자. 이런 식으로 까지 진행하여 직교하는 벡터들을 찾는다. 따라서, 번째에서는 를 에 직교하게 투영하는 를 찾는다.
위의 방법을 코드로 나타내면 다음과 같다.
Example 10.3.2 : 위의 출력 결과에서 알 수 있듯이, 아래의 vlist 에 대해 orthogonalize() 호출하면, 다음과 같은 가 반환된다.
첫 번째 이터레이션에서,
v는 이고vstarlist가 빈 리스트이므로vstarlist에 추가되는 첫 번째 벡터 은 이다.두 번째 이터레이션에서,
v는 이고vstarlist는 만으로 구성되어 있어 의 에 직교하는 투영은 다음과 같다.
세 번째 이터레이션에서,
v는 이고vstarlist는 와 로 구성되어 있어 의 에 직교하는 투영은 이고, 의 에 직교하는 투영은 다음과 같다.
10.3.2 orthogonalize() 가 맞게 동작하는지 증명하기
orthogonalize() 가 제대로 동작하는지 보여주기 위해, 리턴되는 벡터들로 구성된 리스트(vstarlist)의 Span이 입력으로 제공된 벡터들로 구성된 리스트(vlist)의 Span과 동일함을 보여야 한다.
Lemma : orthogonalize를 -원소 리스트 에 적용하면, 번째 이터레이션 후 Span {vstarlist} = Span 이다.
Proof :
벡터 를 양변의 집합에 더하면 다음과 같다.
따라서, 임을 보여주면 된다.
번째 이터레이션에서
project_orthogonal() 을 사용하여 을 계산한다.
위의 식은 벡터들의 임의의 선형결합은 벡터들의 선형결합으로 변환할 수 있고, 그 역도 성립한다.
이러한 직교화(orthogonalization)은 수학자 그램(Gram)과 슈미트(Schmidt)의 이름을 따 Gram-Schmidt 직교화 라고 한다.
위의 식 을 행렬형태로 나타내면 다음과 같다.
우변의 두 행렬은 특수한 형태를 띤다. 첫 번째 행렬은 서로 직교하는 열벡터들을 가진다. 두 번째 행렬은 정방행렬이며 원소는 이면 영(0)인 상삼각(Upper-Triangular) 행렬이다.
Gram-Schmidt Orthogonalization
Gram-Shcmidt Orthogonalization 은 주어진 벡터들 을 생성할 수 있는 직교기저(orthogonal basis) 를 구하는 과정이다.
주어진 벡터들 에 대하여, 이 벡터들을 생성할 수 있는 직교 벡터 들은 다음과 같이 구해진다.
위의 계산을 통해 얻어진 은 서로 직교(orthogonal)하며, 벡터공간 Span 에 대한 직교기저가 된다.
아래의 예제 이미지(출처: Wikipedia) 는 에 대한 직교화 과정을 통해 Gram-Schmidt orthogonormalization 을 구하는 과정이다. 이미지의 의 값은 위의 식에서 이다.

10.4 벡터들의 생성에 속하는 점에 가장 가까운 계산문제 풀기
이제 Span 에 속하며 에 가장 가까운 벡터를 찾는 문제를 해결할 수 있다. 9.3.3 의 Lemma 에 따라, 가장 가까운 벡터는 , 즉 의 상으로의 투영이고, 이것은 이다. 여기서 는 에 직교하는 의 투영이다.
를 찾는 방법은 다음과 같다.
먼저,
orthogonalize()함수를 이용해vlist 의 직교벡터인vstarlist 을 구한다.그 다음,
project_orthogonal()함수를 이용해 를 구한다.
아래의 예제 코드는 vlist=[[8, -2, 2], [4, 2, 4]] 이고 b=[5, -5, 2] 일때 와 를 구한 뒤 가 와 일치하는지 확인하는 코드이다.
이번에는 위 10.1.3에서 제대로 구하지 못했던 , 일 때, 와 를 구한 뒤 가 와 일치하는지 확인해보자.
10.5 orthogonalize() 를 사용하여 다른 문제 풀기
이제, 직교화를 다른 계산문제들에서 어떻게 사용할 수 있는지에 대해 알아 보도록 하자.
Proposition : 서로 직교하는 영(0)이 아닌 벡터들은 선형독립(일차독립)이다.
Proof : 은 서로 직교하는 영이 아닌 벡터들이라 하고, 은 다음 식을 만족하는 계수라고 하자.
계수들 이 모두 영(0) 임을 보여야 한다. 이 인 것을 보이기 위해, 양변에 과의 내적을 취해 보자.
내적 은 이고, 이다. 은 영이 아니므로, 은 영이 아니다. 따라서, 유일한 해는 이다.
마찬가지 방법으로 을 보여줄 수 있다.
10.5.1 기저 계산하기
함수 orthogonalize()는 입력 벡터 vlist의 벡터들이 선형독립이어야 한다는 조건이 없다. 그렇다면 만약 선형독립이 아닐 경우 어떻게 될까?
은 orthogonalize([])에 의해 반환되는 벡터들이라고 하면, 이 벡터들은 서로 직교하며 과 동일한 벡터공간을 생성한다. 하지만, 이 베터들 중 일부는 영벡터 일 수 있다. 는 의 부분집합이며, 영이 아닌 벡터들이라고 하면, Span Span 이다. 왜냐하면 영벡터는 생성에 영향을 주지 않기 때문이다. 또한 벡터들 서로 직교하므로, 의 벡터들은 선형독립이다. 그러므로, 이 벡터들은 Span 에 대한 기저이고, 또한 Span 에 대한 기저이다.
orthogonalize() 함수에서 반환된 vstarlist 에서 기저를 찾는 함수 find_basis()를 구현하면 아래 코드와 같다.
또한, find_basis()를 이용하여 다음의 문제들에 대한 계산도 가능하다.
벡터들로 구성된 리스트의 랭크 찾기
벡터들 이 선형독립인지 테스트 하기
10.5.2 생략
10.5.3 augmented_orthogonalize()
10.2.2 에서 구현한 aug_project_orthogonal(b, vlist)와 마찬가지로 다음을 만족하는 aug_orthogonalize(vlist)를 구현해 보자.
input : 벡터들의 리스트
output : 다음을 만족하는 벡터들의 리스트의 튜플 ()
은 서로 직교하는 벡터들이며 이들의 생성은 Span 과 동일하다.
에 대하여
10.6 직교여공간 - Orthogonal complement
앞에서는 벡터 를 벡터공간 에 직교하게 투영하는 것에 대해 알아보았다. 이번에는 전체 벡터공간을 또 다른 벡터공간에 직교하게 투영하는 것에 대해 알아보자.
10.6.1 직교여공간의 정의
Definition : 는 실수상의 벡터공간이라 하고, 는 의 부분공간이라 하자. 의 에 대한 직교여공간 은 다음을 만족하는 집합 라고 정의한다.
집합 는 위의 정의에 의해 의 부분집합이며, 다음과 같이 말할 수도 있다.
Lemma : 는 의 부분공간이다.
Proof : 내의 임의의 두 벡터 과 에 대해, 도 또한 에 속한다는 것을 보여 준다. 의 정의에 의해 과 는
(1) 둘 다 벡터공간 에 속하고,
(2) 에 속하는 모든 벡터에 직교한다.
(1) 에 의하면 두 벡터의 합은 에 속한다. (2) 를 9.3.2의 Orthogonality Property 2 에 대입하면 이 합은 에 속하는 모든 벡터에 직교한다. 따라서 는 에 속한다.
마찬가지로 임의의 벡터 와 임의의 스칼라 에 대해, 가 에 속한다는 것을 보여야 한다. 는 벡터공간 에 속하므로, 도 또한 에 속한다. 는 에 속하는 모든 벡터에 직교하므로, 9.3.2의 Orthogonality Property 1 에 따르면 도 또한 에 속하는 모든 벡터에 직교한다. 따라서 는 에 속한다.
Example 10.6.3 : 이라고 하자. 는 에 속하는 의 직교여공간으로 나타내보자. 어떤 벡터들이 에 대한 기저를 형성할까?
내의 모든 벡터는 형태를 가진다. 그러므로, 형태의 임의의 벡터는 내의 모든 벡터에 직교한다.
예를 들어, 에 속하는 모든 벡터는 내의 모든 벡터에 직교하므로, 은 의 부분공간이며 에 속하는 의 직교여공간 이다.
이고 라는 것을 알고 있으며, 은 선형독립이므로, 이고 라고 할 수 있다. 또한 은 선형독립이고, 이다. 그러므로, 은 와 동일하다.
10.6.2 직교여공간과 직합(Direct sum)
이제, 직교여공간과 직합(direct sum) 사이의 연관성을 알아보자.
Lemma : 는 의 에 대한 직교여공간이라고 하면, 에 속하는 유일한 벡터는 영벡터이다.
Proof : 에 속하는 벡터 는 내의 모든 벡터에 직교한다. 만약 도 또한 에 속하면, 는 자기자신과 직교한다. 즉, 이다. 9.1.1 의 의 성질에 의하면 가 영벡터임을 의미한다.
따라서, 위의 Lemma에 의해 아래와 같이 직합 를 형성할 수 있다. (7.3.1 참고)
아래의 Lemma는 가 와 의 직합이고, 따라서 와 는 의 여부분공간(complemantary subspace) 이라는 것을 보여준다.
Lemma : 만약 의 에 대한 직교여공간이 이면,
Proof : 증명하는데 두 가지 방법이 있다.
의 모든원소는 와 에 대해 형태를 가진다. 와 는 둘 다 벡터공간 의 부분집합이므로, 합 는 에 속한다. 즉, 임을 보여준다.
에 속하는 임의의 벡터 에 대해, 라고 나타내자. 는 의 상으로의 투영이고 는 의 에 직교하는 투영이다. 는 에 속하고 는 에 속한다. 따라서, 는 에 속하는 벡터와 에 속하는 벡터의 합이다. 즉, 임을 보여준다.
10.6.3 생성 또는 아핀 hull로 주어진 평면의 법선
"평면의 법선(normal to a plane)" 에서 법선(normal) 이란, 수직이라는 의미이다.
예를들어 두 개의 -벡터 과 의 생성(Span)된 평면이라고 하자. 이 경우, 이 평면은 차원의 벡터공간 이다. 은 에 직교하는 영이 아닌 벡터라고 하면, Span 은 에 속하는 의 직교여공간의 부분공간이다. 또한, 7.3 직합 에서 Direct-Sum Dimension 에 의하면, 직교여공간의 차원은 이다. 따라서, 직교여공간은 Span 이다. Span 에 속하는 임의의 영이 아닌 벡터는 법선 역할을 한다. 보통 법선벡터는 Span 에 속하는 이 인 벡터를 말한다.
Example 10.6.6 : 위의 10.4에서 예제코드에서도 보았듯이, Span 에 직교하는 하나의 영이 아닌 벡터는 이고, 이것은 법선벡터이다. 이 인 법선을 구하는 방법은 의 으로 나누면 된다. 따라서, 법선은 이다.
10.6.4 직교여공간, 영공간, 소멸자
는 상의 행렬이라 하면, 의 영공간(null space)은 이 되는 -벡터들 의 집합이다. 행렬 -벡터 곱셈의 도트곱 정의에 의하면, 의 각 행과의 도트곱이 영이 되는 -벡터들 의 집합이다. 상의 벡터들에 대한 내적은 도트곱이므로, 에 속하는 Row 의 직교여공간은 Null 임을 의미한다. 또한, Null 는 Row 의 소멸자(annihilator) 이다. 이것은 의 임의의 부분공간 에 대해 에 속하는 의 직교여공간은 소멸자 임을 의미한다.
따라서, 상의 임의의 벡터공간 와 임의의 부분공간 에 대한 의 에 대한 직교여공간()의 직교여공간() 은 자신이라는 것을 알 수 있다.
10.6.5 방정식으로 주어진 평면의 법선
다시 평면의 법선을 찾는 문제로 가보자. 평면은 다음과 같이 선형방정식에 대한 해집합으로 주어진다.
4.6.1에서 보았듯이, 해집합은 아래의 동차선형방정식에 대한 해집합의 평행이동이라 할 수 있다.
하고, 해집합 은 소멸자 이다. 소멸자 에 속하는 벡터들로 구성된 평면의 법선을 찾고자 한다. 소멸자 에 직교하는 벡터들의 집합은 소멸자의 소멸자 즉, 이다. 이것은 자기자신 이다. 따라서, 법선이 될 수 있는 하나의 후보 벡터로는 가 된다.
10.6.6 직교여공간 계산하기
의 부분공간 에 대한 기저 와 에 대한 기저 이 있다고 해보자. 에 속하는 직교여공간에 대한 기저를 위에서 구현한 orthogonalize() 함수를 이용해 계산해보자.
입력벡터들 vlist=[] 의 출력 벡터인 vstarlist=[]은vlist와 마찬가지로 동일한 공간, 즉 차원이 인 벡터공간을 생성한다. 따라서, 중 개는 영이 아니다. 또한, 는 와 동일한 공간을 가지며, 는 선형독립이기 때문에 모두 영이 아니다. 나머지 벡터들 중 개는 영이 아니다. 따라서 모든 원소는 에 직교하며 에 속하는 모든 벡터에 직교한다. 따라서, 의 직교여공간에 있다. 직교여공간은 차원을 가진다.
아래의 예제코드는 직교여공간에 대한 기저를 구하는 코드이다.
Example 10.6.7 : 위의 find_orthogonal_complement() 함수를 이용해 에 속하는 Span 의 직교여공간에 대한 기저를 찾아보자. 에 대한 표준 기저, 즉, 을 사용한다.
출력 결과에서 처음과 두번째 벡터는 Span 의 원소이고, 네번째와 다섯번째는 영벡터이다. 따라서 위의 직교여공간의 기저는 이다.
10.7 인수분해
이제 앞에서 배운 내용들을 토대로 행렬 인수분해에 대해 살펴보자. 행렬 인수분해는 수학적 및 계산적 역할을 한다.
수학적(Mathematical) : 행렬 인수분해는 행렬의 본질에 대한 통찰(?)을 제공한다. 행렬에 대해 생각하는 새로운 방식을 제시한다.(나도 이해할 수 있겠지?...)
계산적(Computational) : 행렬 인수분해는 행렬이 포함된 계산문제들에 대한 해를 계산하는 방안을 제공한다.
10.7.1 직교 및 열-직교 행렬
Definition : 서로 직교하는 벡터들은 만약 이 모두 1이면 정규직교(orthonormal) 한다고 한다. 행렬은 만약 그 열들이 정규직교하면 열-직교(column-orthogonal) 라고 한다. 정방 열-직교행렬(square column-orthogonal matrix)은 직교행렬 이라 한다.
는 열-직교 행렬이라 하고 그 열들을 이라 하고, 의 행들 또한 정규직교이다. 아래와 같이 행렬곱셈 를 해보자.
의 번째 원소는 행렬의 행- 와 행렬의 열- 의 도트곱이다. 따라서, 원소는 이다. 만약 이면, 이며 즉 의 제곱이므로 이다. 만약 이면, 서로 직교하는 두 벡터들의 내적이므로 그 값은 영(0)이 된다. 따라서 는 단위행렬(Identity Matrix) 이 된다.
Lemma : 만약 가 열-직교행렬이면 는 단위행렬 이다.
Corollary(직교행렬의 역) : 만약 가 직교행렬이면, 그 역행렬은 이다.
10.7.2 행렬의 인수분해 정의하기
Definition : 행렬 의 인수분해는 이다. 여기서, 는 열-직교 행렬 이고, 은 상삼각행렬이다.
Lemma : 의 인수분해에서, 만약 의 열들이 선형독립이면 Col Col 이다.
파이썬의 numpy모듈에서는 numpy.linalg.qr를 통해 QR 분해를 계산할 수 있다(직접 구현하려고 했으나.. 시간이 부족했습니다..ㅜㅜ)
10.8 인수분해를 사용하여 행렬방정식 풀기
10.8.1 정방행렬인 경우
실수상의 행렬방정식 를 고려해보자. 행렬 는 정방행렬이고 의 열들은 선형독립인 경우, 인수분해를 기반으로 하여 이 방정식을 푸는 방법이 있다.
의 열들이 선형독립이라 하고 은 의 인수분해라고 해보자. 이때, 다음 방정식을 만족하는 벡터를 찾고자 한다.
에 을 대입하면 다음을 얻는다.
양변의 항의 왼쪽에 을 곱하면 다음이 얻어진다.
의 열들은 정규직교이므로 는 단위행렬 이고 다음과 같이 쓸 수 있다.
따라서 를 만족하는 임의의 벡터 는 또한 식 를 만족해야 한다.
10.8.2 정방행렬인 경우 솔루션의 정확성
에 대한 임의의 해는 에 대한 해라는 것은 보여주었다.
에 대한 해는 에 대한 해라는 것을 보여야 한다.
Theorem : 는 정방행렬이고 그 열들은 선형독립이라고 하면, 10.8.1 에서 얻어진 벡터 은 방정식 를 만족한다.
Proof :
양변의 항의 왼쪽에 를 곱하면 다음을 얻는다.
이것은 다음과 동일하다.
는 정방행렬이기 떄문에 도 정방행렬이다. 이고 다음이 성립한다.
위의 10.8.1과 10.8.2 에서는 다음과 같이 특수한 경우 의 행렬방정식 푸는 방법이다.
필드가 일 때
의 열들이 선형독립일 때
가 정방행렬일 때
10.8.3 최소제곱 문제
필드는 이고 의 열들은 선형독립이라고 가정하자. 는 행렬이라 하고 함수 는 로 정의하자. 정의역은 이고, 정의역의 차원은 이다. 공역의 차원은 이다. 의 행 개수가 열 개수가 많은 경우 즉 이면 공역의 차원은 치역의 차원보다 더 크다. 따라서, 공역에는 치역에 없는 벡터들이 있으므로 는 전사함수가 아니다. 벡터 는 이러한 벡터 중 하나라고 해보자. 즉 에 대한 해는 없다. 이러한 경우 두 가지 문제를 생각해 볼 수 있다.
의 열들의 선형결합 중에서 에 가장 가까운 벡터 찾기
가장 가까운 벡터를 선형결합으로 표현할 수 있는 계수(좌표)들 찾기
직교화는 첫 번째 문제를 풀 수 있다. 에 가장 가까운 점은 이고 , 이것은 의 열공간상으로의 투영이다.
두 번째 문제는 최소제곱(least squares)법 을 이용하여 해결할 수 있다. 최소제곱법은 주어진 벡터 에 대해서 벡터 를 잉여벡터(residual vector, 오차 error라고도 함) 의 즉, 를 최소화 하는 벡터 를 찾는 것이다.
10.8.4 열-직교해렬의 열들에 대한 좌표 표현
여기서 잊지말아야 할것은 정방행렬에 대한 문제가 아닌 인 행의 개수가 열의 개수보다 많을 때의 경우에 대한 설명이다.
Lemma : 는 열-직교 기저라 하고 Col 라고 하면, 정의역이 의 행-라벨 집합과 동일한 임의의 벡터 에 대해, 는 의 열들에 대한 의 좌표 표현이고, 는 이다.
Proof : 라고 나타내면, 는 내에 있으므로, $Qq_1, … , q_n$ 의 선형결합으로 표현될 수 있다.
따라서, 의 좌표 표현은 이다. 이제 이 벡터가 와 동일하다는 것을 보여야 한다. 앞의 10.7.1 에서 보았듯이 행렬-벡터 곱셈의 도트곱으로 나타내면 의 원소 는 의 열 와 의 도트곱이다. 이 도트곱은 와 동일하다는 것을 보여준다.
에 대해, 이기 떄문에 이것은 가 에 대한 의 좌표표현이라는 것을 알 수 있다.
벡터의 좌표표현에서 벡터 자체를 얻기 위해서는 열들이 기저를 형성하는 행렬, 여기서는 를 곱한다. 따라서, 는 자신이다.
10.8.5 의 행 개수가 열 개수보다 더 많을 때 QR 분해를 이용해 풀기
최소제곱 문제와 마찬가지로 를 최소화 하는 벡터 를 찾는 것이다. 이것은 는 상으로의 투영 와 동일하다. 여기서 는 의 Col 열공간 이다.
'Linear Algebra > Coding the Matrix' 카테고리의 다른 글
| [코딩더매트릭스]Chap09 - 내적 Inner Product (0) | 2018.05.17 |
|---|---|
| [코딩더매트릭스]Chap08 - 가우스 소거법 Gaussian Elimination (0) | 2018.05.04 |
| [코딩더매트릭스]Chap07 - 차원 Dimension (0) | 2018.05.02 |
| [코딩더매트릭스]Chap06 - 기저 Basis (0) | 2018.04.19 |
| [코딩더매트릭스]Chap05 - 행렬 The Matrix (2) | 2018.03.14 |