| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 알고리즘
- C
- graph
- python
- 텐서플로
- recursion
- hive
- scrapy
- 딥러닝
- collections
- effective python
- 하둡2
- 선형대수
- hadoop2
- Sort
- HelloWorld
- Java
- GRU
- 파이썬
- codingthematrix
- RNN
- 주식분석
- LSTM
- 하이브
- 그래프이론
- C언어
- NumPy
- tensorflow
- 코딩더매트릭스
- yarn
- Today
- Total
EXCELSIOR
Loss functions for Regression 본문
Loss functions for Regression
1. Loss functions for regression
- Mean Absolute Error (MAE)
- Mean Absolute Percentage Error (MAPE)
- Mean Squared Error (MSE)
- Root Mean Squared Error (RMSE)
- Huber Loss
- Log-Cosh Loss
2. Mean Absolute Error (MAE, L1 Loss)
- MAE는 가장 단순한 형태의 loss function이라고 할 수 있음
- 각각의 실제값($y_i$)과 예측값($\hat{y}_i$) 간의 차이의 절대값을 구한 후 평균을 구한것을 MAE라 함
- 수식은 다음과 같음
$$
\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left| y_i - \hat{y}_i \right|
$$

- 위의 그래프에서 확인할 수 있듯이, MAE loss를 L1 loss라고 부르기도 함
2.1 Advantages
- Loss를 계산하기 매우 간단한 구조에 해당함
- 따라서, 계산 비용(computational cost)이 높지 않음
- 제곱을 취해주는 MSE 보다 Outlier에 대해 Robust 함
2.2 Drawbacks
- 스케일(scale)에 대해 의존적임
- $y_i = 300$, $\hat{y}_i = 500$ 에 대한 에러비율(40%) 과, $y_i = 2000$, $\hat{y}_i = 1800$ 에 대한 에러비율(10%)에 대해 동일한 loss가 구해지게 됨
- 절대값을 씌우기 때문에, 음수인지 양수인지에 대해 파악할 수 없음
- 위의 그래프에서 확인할 수 있듯이, backpropagation시 모든 loss에 대해 동일한 가중치(gradient)가 적용됨 → 수렴하는 데 오래 걸릴 수 있음
3. Mean Absolute Percentage Error (MAPE)
- MAPE는 MAE를 백분률로 변환해준 것
- 따라서, MAPE는 스케일(scale)에 의존적이지 않음
- 수식은 다음과 같음
$$
\text{MAPE} = \frac{1}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right| \times 100%
$$

3.1 Advantages
- 모든 에러에 대해 정규화(normalization)되기 때문에, 스케일에 의존적이지 않음
- MAE와 마찬가지로 outlier에 대해 robust 함
3.2 Drawbacks
- MAPE의 가장 치명적인 단점은 실제값 $y_i = 0$ 인 경우, 분모가 $0$이 되기 때문에 계산이 불가능해짐
- 실제값 $y_i$에 따라 loss 값이 달라질 수 있음
- 예를들어, $y_i=100, \hat{y}_i=70$의 MAPE는 $0.3$ 의 값을 가지고, $y_i=40, \hat{y}_i=70$ 의 MAPE 값은 0.75를 가지게 됨
4. Mean Squared Error (MSE, L2 Loss)
- MSE는 각각의 실제값($y_i$)과 예측값($\hat{y}_i$) 간의 차이(에러)에 대해 제곱을 한 후 평균을 계산해 줌
- MSE는 에러의 제곱에 비례하기 때문에, 에러가 큰 값에 대해 상대적으로 더 높은 패널티를 부여함
- 수식은 다음과 같음
$$
\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2
$$
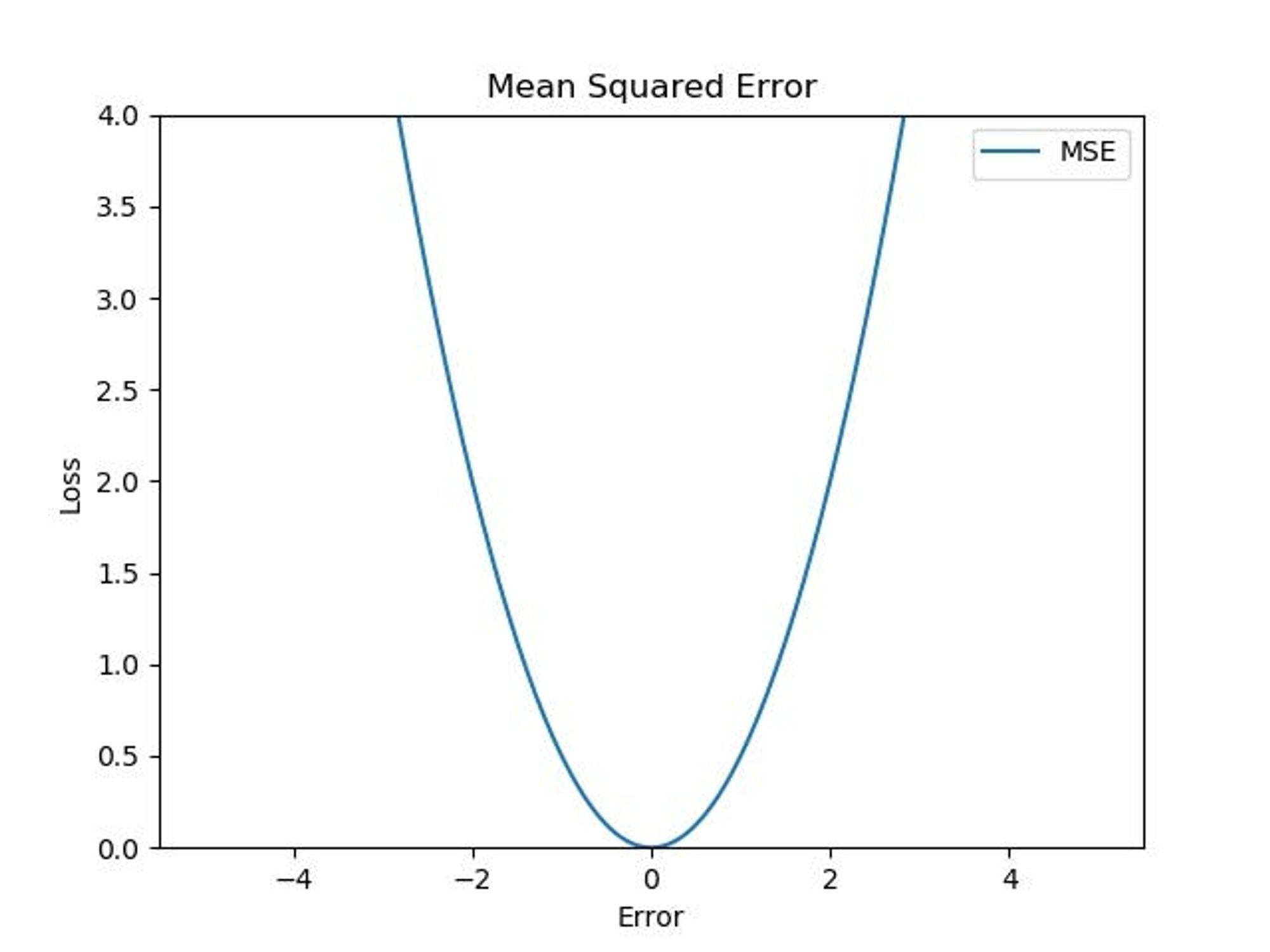
- 위의 식을 살펴보면, 분산과 동일한 구조를 가지는 것을 확인할 수 있음:
- 분산은 아래의 식과 같이, 각 데이터 포인트와 평균의 차이를 제곱한 후 평균을 계산해 줌
- 분산은 데이터가 평균으로부터 얼마나 퍼져 있는지를 나타내는 통계치라고 할 수 있음
- $$
\text{Var}(y) = \frac{1}{n} \sum_{i=1}^{n} \left(y_i - \bar{y}\right)^2
$$
- 즉, MSE 또한 분산과 마찬가지로 예측값이 실제값으로부터 얼마나 퍼져있는지를 나타내는 지표라고 할 수 있음
4.1 Advantages
- 제곱항을 통해서 오차의 평균이 0이 되는것을 방지해 줌
- 예를들어, 오차가 $+2, -2$ 인 경우에 제곱을 하지않고 오차의 평균을 구하게 되면 $0$이 되는 문제가 발생함
- 위의 그래프에서 처럼, 작은 오차의 경우에는 MSE의 기울기(gradient)가 감소하므로, 최소값에 효율적으로 수렴할 수 있음
4.2 Drawbacks
- 오차를 제곱하기 때문에, $\left| y_i - \hat{y}_i \right| > 1$ 인 경우 값이 기하급수적으로 커지게 됨
- 따라서, backpropagation 시에 exploding 하는 경우가 발생할 수 있음
- 또한, outlier에 민감하게 반응하므로, 이 outlier가 학습에 큰 영향을 미칠 수 있음
5. Root Mean Squared Error (RMSE)
- RMSE는 MSE에 제곱근(square root)을 취해줌
- 제곱근을 취해줌으로써, linear scoring method가 되지만 MSE 처럼 오차가 큰 값에 대해 더 많은 패널티를 부여해줄 수 있음
- 수식은 다음과 같음
$$
\text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left( y_i - \hat{y}_i \right)^2}
$$
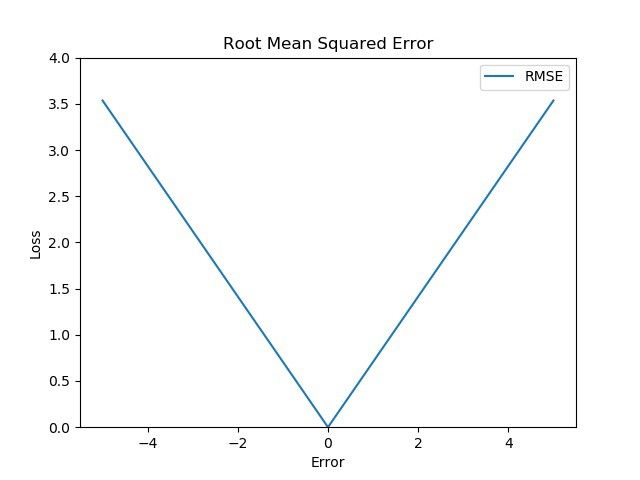
5.1 Advantages
- MSE에 비해, $\left| y_i - \hat{y}_i \right| > 1$ 인 경우 값이 기하급수적으로 커지게 되는 문제를 완화해줄 수 있음
- MAE와 마찬가지로 outlier에 대해 robust함
5.2 Drawbacks
- MAE처럼 0 근처에서도 gradient 값이 거의 유지되기 때문에 수렴이 어려울 수 있음
6. MAE vs MSE vs RMSE vs MAPE
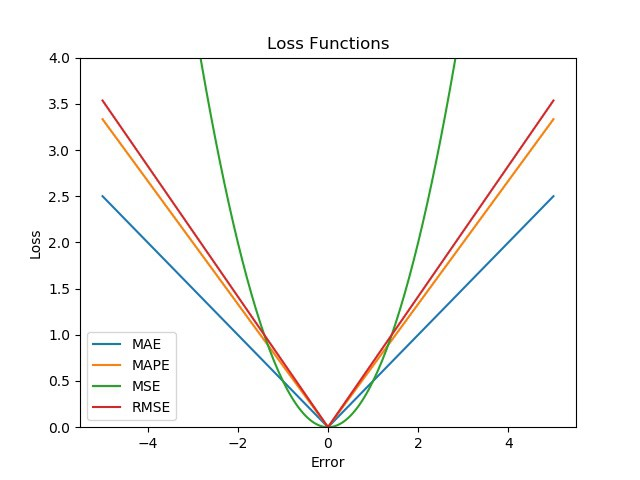
7. Huber Loss
- Huber Loss는 MSE와 MAE를 반영한 loss function이라고 할 수 있음
- 하이퍼파라미터인 일정한 범위 $\delta$에 대해 $\delta$안에 속하면 오차를 제곱하고, 그 밖에 있으면 오차의 절대값을 구해줌
$$
l \left(y_i, \hat{y}_i \right) = \begin{cases}
\frac{1}{2} \left( y_i - \hat{y}_i \right)^2, & \text{for } \left| y_i - \hat{y}_i \right| < \delta \
\delta \big( \left| y_i - \hat{y}_i \right| - \frac{1}{2} \delta \big), & \text{otherwise}
\end{cases}
$$
- 위의 식에서 $\delta = 1$ 경우, SmoothL1Loss 라고 함
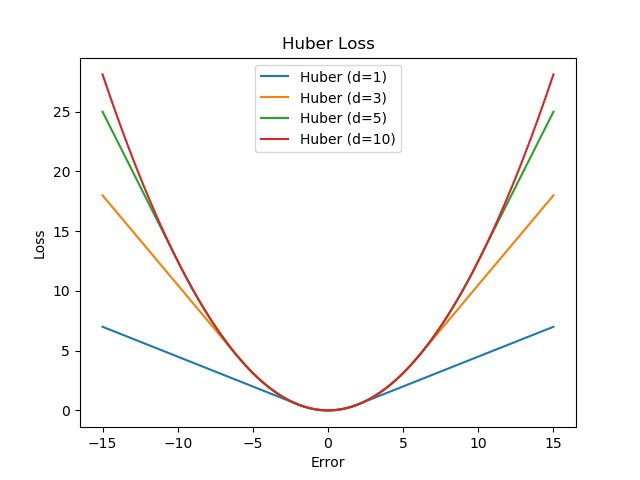
7.1 Advantages
- 하이퍼파라미터인 $\delta$를 통해 Loss를 조절할 수 있음
- $\delta$ 이상의 값인 outlier에 대해서는 MSE에 비해 더 robust함
- $\delta$ 이하의 값에 대해서는 backpropagation시 더 잘 수렴할 수 있음
7.2 Drawbacks
- $\delta$ 라는 조건이 붙으므로, MAE나 MSE에 비해 계산 비용이 상대적으로 높음
- 하이퍼파라미터 $\delta$에 대한 최적값도 구해야하는 번거로움이 있음
8. Log-Cosh Loss
- Log-Cosh Loss는 Huber Loss처럼, linear한 부분과 quadratic한 부분을 합친 loss function이라 할 수 있음
- 가장 큰 차이점은, Huber Loss는 1차 미분만 가능한데 비해 Log-Cosh Loss는 2차미분이 가능함
$$
\text{Logcosh}(y_i, \hat{y}_{i}) = \sum_{i=1}^{n} \log{\big( \cosh(y_i - \hat{y}_i) \big)}
$$
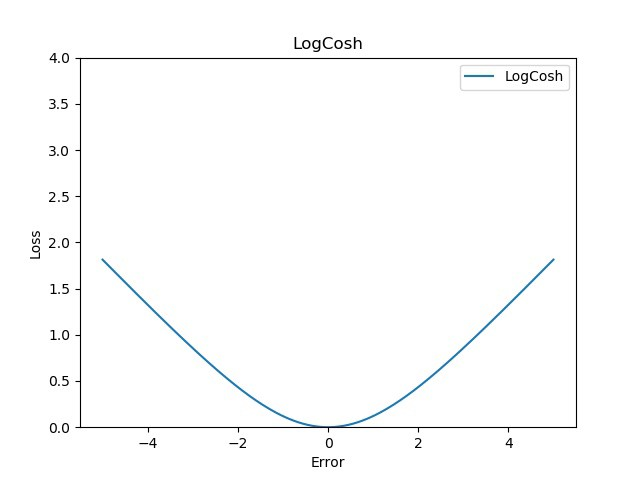
8.1 Advantages
- 2차 미분이 가능함
- Huber Loss에 비해 계산 비용이 적음
8.2 Drawbacks
- Huber Loss에 있는 하이퍼파라미터 $\delta$가 없기 때문에, less adaptive 함
9. Comparison of Loss Functions

10. Conclusion
Loss Function 중 Regression과 관련된 Loss function을 살펴보았다. 이 글을 정리한 이유는 얼마전 Regression 모델을 PyTorch DistibutedDataParallel(DDP)로 학습시켜야 했는데, 학습중 NaN 값이 나타나는 문제가 발생했다. 난 당연히 DDP를 처음 써봐서 '프로그래밍을 잘못해줬구나' 라고 생각했는데, 디버깅을 하고 보니 사용했던 MSE loss가 기하급수적으로 증가해서 NaN값이 발생하는 것이었다. 이 문제를 해결하고자 Regression과 관련된 Loss function을 찾던 중 Rohan Hirekerur 의 블로그를 보게 되었고, 이를 기반으로 정리하게 되었다.
'DeepLearning > 개념' 카테고리의 다른 글
| 08. 오토인코더 (AutoEncoder) (7) | 2018.11.03 |
|---|---|
| 07-3. 순환 신경망 LSTM, GRU - (3) (4) | 2018.10.29 |
| 07-2. 순환 신경망 (RNN, Recurrent Neural Network) - (2) (0) | 2018.10.26 |
| 07-1.순환 신경망(RNN, Recurrent Neural Network) - (1) (2) | 2018.10.25 |
| 06. 합성곱 신경망 - Convolutional Neural Networks (9) | 2018.10.19 |




