| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- yarn
- GRU
- 하둡2
- effective python
- hive
- 하이브
- tensorflow
- graph
- recursion
- 파이썬
- Java
- Sort
- 코딩더매트릭스
- 딥러닝
- C언어
- LSTM
- NumPy
- 알고리즘
- collections
- hadoop2
- 텐서플로
- C
- 선형대수
- python
- scrapy
- HelloWorld
- 그래프이론
- RNN
- codingthematrix
- 주식분석
- Today
- Total
EXCELSIOR
05-2. 심층 신경망 학습 - 배치 정규화, 그래디언트 클리핑 본문
저번 포스팅 05-1. 심층 신경망 학습에서는 DNN 학습에 있어서 적절한 활성화 함수 및 가중치 초기화 방법에 대해 알아보았다. 이번 포스팅에서는 그래디언트 소실(vanishing gradient)과 폭주(exploding) 문제를 해결하는 방법인 배치 정규화(BN, Batch Normalization)
1. 배치 정규화(BN, Batch Normalization)
05-1. 심층 신경망 학습에서는 활성화 함수로는 ReLU를 사용하고 He 초기화를 통해 학습 초기 단계에서의 그래디언트 소실/폭주 문제를 줄일 수 있었지만, 이러한 문제가 학습하는 동안에 또 다시 발생할 가능성이 있다.
2015년 Sergety Ioffe와 Christian Szegedy는 'Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift'라는 논문에서 배치 정규화(BN, Batch Normalization)를 제안했다. 배치 정규화는 각 층의 활성화 함수의 출력값 분포가 골고루 분포되도록 '강제'하는 방법으로, 각 층에서의 활성화 함수 출력값이 정규분포(normal distribution)를 이루도록 하는 방법이다.
즉, 학습하는 동안 이전 레이어에서의 가중치 매개변수가 변함에 따라 활성화 함수 출력값의 분포가 변화하는 내부 공변량 변화(Internal Covariate Shift) 문제를 줄이는 방법이 바로 배치 정규화 기법이다.
배치 정규화는 아래의 그림과 같이 미니배치(mini-batch)의 데이터에서 각 feature(특성)별 평균(, mean)과 분산(, variance)을 구한 뒤 정규화(normalize) 해준다.
일반적으로 배치 정규화는 아래의 그림과 같이 Fully Connected(FC)나 Convolutional layer 바로 다음, 활성화 함수를 통과하기 전에 배치 정규화(BN)레이어를 삽입하여 사용한다.
배치 정규화는 미니배치(mini-batch)를 단위로 데이터의 분포가 평균(, mean)이 0, 분산(, variance)이 1이 되도록 정규화(normalization)한다. 수식은 다음과 같다.
Input : 미니배치 개의 입력 데이터, 학습 될 파라미터인
Output :
: 미니배치 에 대한 평균
: 미니배치 에 대한 표준편차
: 미니배치 데이터 개수
: 평균이 0, 분산이 1로 정규화된 입력 데이터
: 정규화된 데이터에 대한 스케일(scale) 조정 파라미터
: 정규화된 데이터에 대한 이동(shift) 조정 파라미터
: 분모가 0이 되는 것을 막기 위한 작은 숫자 ()
: 연산의 출력 결과
1.1 Scale()과 Shift()를 해주는 이유
위의 식에서 입력 데이터()에 대해 정규화(normalization, )를 하게 되면, 의 값이 대부분 0에 가까운 값이 될 것이다. 만약, 이러한 정규화된 입력 데이터 가 시그모이드(sigmoid) 활성화 함수의 입력값으로 들어가게 되면, 비선형(nonlinearity) 함수인 sigmoid가 선형(linearity)구간에 빠지게 된다(sigmoid 함수는 0 부근에서 선형성을 띤다). 이러한 문제를 해결하기 위해서 아래의 식과 같이 정규화된 입력 데이터 에 scaling과 shifting해주는 와 를 적용 해준다.
와 를 다르게 표현하면 에 대한 가중치() 와 편향(bias, )라고 볼 수 있으며, 와 는 초기값으로 으로 시작해(즉, 초기에는 입력값 그대로 학습), 학습 과정에서 역전파(backprop)에 의해 적합한 값으로 조정된다.
1.2 테스트(추론) 단계에서의 BN
테스트 단계(추론 단계처럼 데이터가 하나씩 주입된다고 가정)나 추론 단계에서는 평균()과 표준편차()를 계산할 미니배치가 없기 때문에 전체 Training Set의 평균과 표준편차를 사용한다. 하지만, 엄청나게 많은 전체 Training set에 대한 평균과 표준편차를 계산하기에는 무리기 때문에, 아래의 식과 같이 각 개의 미니배치에 대한 평균과 표준편차를 이용해 전체 Training Set의 평균과 표준편차를 대신한다.
위와 같은 방법 대신, 모델 학습 단계에서 지수 감소(exponential decay) 이동 평균법(moving average)을 사용하여 평균과 표준편차를 계산할 수 있다.
위의 식에서 는 모멘텀(momentum)값으로 일반적으로 1에 가까운 0.9, 0.99, 0.999로 설정한다. 이러한 moving mean과 moving stddev는 학습 단계에서 매 미니배치마다 업데이트 해준다.
1.3 BN의 장점
Batch Normalization(BN)은 논문에서 실험했던 모든 DNN의 성능이 크게 향상 시켰다. BN은 다음과 같은 장점들이 있다.
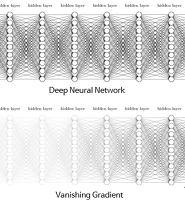
tanh나 sigmoid 같은 활성화 함수에 대해 그래디언트 소실(vanishing gradient)문제가 감소한다.
가중치 초기화에 덜 민감하다. 가중치 초기값에 크게 의존하지 않기 때문에 05-1. 심층 신경망 학습에서 알아본 가중치 초기화 기법에 대해 크게 신경 쓰지 않아도 된다.
학습률(learning rate)를 크게 잡아도 gradient descent가 잘 수렴한다.
오버피팅을 억제한다. BN이 마치 Regularization 역할을 하기 때문에 드롭아웃(Dropout)과 같은 규제기법에 대한 필요성이 감소한다. 하지만, BN로 인한 규제는 효과가 크지 않기 때문에 드롭아웃을 함께 사용하는 것이 좋다.
1.4 텐서플로에서 Batch Normalization 구현하기
텐서플로(TensorFlow)에서는 tf.nn.batch_normalization()과 tf.layers.batch_normalization()을 통해 두 개의 Batch Normalization을 제공한다. 하지만, tf.nn.batch_normalization은 평균과 표준편차(학습할 때는 미니배치, 테스트할 때는 전체 데이터셋)를 직접 계산한 뒤 인자로 전달해줘야 하며, scaling과 shifting을 위한 를 만들어 줘야한다. 반면, tf.layers.batch_normalization은 이러한 작업들을 모두 처리해 주기 때문에 이것을 사용하는 것이 좋다.
이제, tf.layers.batch_normalization을 이용하여 MNIST 데이터셋을 분류하는 DNN을 구현해 보도록 하자. DNN의 구성은 아래의 그림과 같이 784개의 입력층(input) → 300개 노드의 은닉층(hidden1) → 100개 노드의 은닉층(hidden2) → 10개의 출력층(output)으로 구성되어 있다.
아래에 대한 전체 코드는 ExcelsiorCJH GitHub에서 확인할 수 있다.
1) MNIST DataSet Load
먼저, 학습과 테스트에 사용할 MNIST 데이터셋을 로드한 뒤 랜덤하게 미니배치 크기만큼 가져오기 위한 shuffle_batch() 함수를 구현하자.
import tensorflow as tf
# MNIST Load
(train_x, train_y), (test_x, test_y) = tf.keras.datasets.mnist.load_data()
# Train & TestSet reshape
train_x = train_x.astype(np.float32).reshape(-1, 28*28) / 255.
train_y = train_y.astype(np.int32)
test_x = test_x.astype(np.float32).reshape(-1, 28*28) / 255.
test_y = test_y.astype(np.int32)
# Split Validation set from Train set
valid_x, train_x = train_x[:5000], train_x[5000:]
valid_y, train_y = train_y[:5000], train_y[5000:]
# mini-batch
def shuffle_batch(inputs, labels, batch_size):
rnd_idx = np.random.permutation(len(inputs))
n_batches = len(inputs) // batch_size
for batch_idx in np.array_split(rnd_idx, n_batches):
batch_x, batch_y = inputs[batch_idx], labels[batch_idx]
yield batch_x, batch_y2) NN 구성하기
tf.layers.batch_normalization()처럼 배치 정규화가 반복해서 사용하기 때문에 코드 중복을 줄이기 위해 Python의 내장 모듈인 functools모듈 안에 있는 partial()함수를 사용해서 배치 정규화를 적용한다.
tf.layers.batch_normalization로 배치 정규화를 사용할 경우, '1.2 테스트(추론) 단계에서의 BN'에서 살펴본 moving mean과 moving variance를 업데이트를 해주기 위해 tf.GraphKeys.UPDATE_OPS를 사용해야 한다
from functools import partial
################
# layer params #
################
n_inputs = 28*28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
batch_norm_momentum = 0.9
# input layer
inputs = tf.placeholder(tf.float32, shape=[None, n_inputs], name="X")
# output layer
labels = tf.placeholder(tf.int32, shape=[None], name='labels')
# BN에 사용하기 위한 학습 유무
training = tf.placeholder_with_default(False, shape=[], name="training")
with tf.name_scope('dnn'):
# batch normalization layer using partial
batch_norm_layer = partial(
tf.layers.batch_normalization,
training=training,
momentum=batch_norm_momentum)
# 1st - hidden
hidden1 = tf.layers.dense(inputs, n_hidden1, name="hidden1")
# batch norm
bn1 = batch_norm_layer(hidden1)
# activation function
bn1_act = tf.nn.elu(bn1)
# 2nd - hidden
hidden2 = tf.layers.dense(bn1_act, n_hidden2, name="hidden2")
bn2 = batch_norm_layer(hidden2)
bn2_act = tf.nn.elu(bn2)
# outputs
logits_before_bn = tf.layers.dense(bn2_act, n_outputs, name="outputs")
logits = batch_norm_layer(logits_before_bn)
with tf.name_scope('loss'):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits)
loss = tf.reduce_mean(xentropy, name='loss')
################
# Hyper-params #
################
learning_rate = 0.01
n_epochs = 5
batch_size = 50
# moving mean & variance update
update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
with tf.control_dependencies(update_ops):
with tf.name_scope('train'):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train_op = optimizer.minimize(xentropy)
with tf.name_scope('eval'):
correct = tf.nn.in_top_k(logits, labels, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))3) 학습 시키기(Training)
with tf.Session() as sess:
tf.global_variables_initializer().run()
for epoch in range(n_epochs):
for batch_x, batch_y in shuffle_batch(train_x, train_y, batch_size):
sess.run(train_op, feed_dict={inputs: batch_x,
labels:batch_y,
training: True})
# validation
accuracy_val = accuracy.eval(feed_dict={inputs: valid_x, labels: valid_y})
print('epoch: {:03d}, valid. Acc: {:.4f}'.format(epoch, accuracy_val))
"""
epoch: 000, valid. Acc: 0.9582
epoch: 001, valid. Acc: 0.9728
epoch: 002, valid. Acc: 0.9740
epoch: 003, valid. Acc: 0.9790
epoch: 004, valid. Acc: 0.9798
"""2. 그래디언트 클리핑 (Gradient Clipping)
그래디언트 클리핑(Gradient Clipping)은 그래디언트 폭주(exploding gradient) 문제를 줄이는 방법이며, 역전파(backprop) 단계에서 그래디언트 값이 아래의 그림과 같이 특정 임계값(threshold)을 넘지 않도록 잘라내는 방법이다.
2.1 텐서플로에서 그래디언트 클리핑 구현하기
텐서플로에서는 tf.clip_by_value를 이용해 그래디언트 클리핑을 구현할 수 있다. 아래의 예제는 '1.4 텐서플로에서 Batch Normalization 구현하기'에서 사용한 MNIST 데이터셋을 분류하는 간단한 분류기를 구현한 뒤에 그래디언트 클리핑을 적용한 예제이다. 아래의 전체 코드는 ExcelsiorCJH GitHub에서 확인할 수 있다.
tf.clip_by_value를 사용하려면, 아래의 코드에서 옵티마이저(tf.train.GradientDescentOptimizer)에 사용해야 한다. '1.4 텐서플로에서 Batch Normalization 구현하기'에서는 옵티마이저의 minimize()함수를 이용해 그래디언트 계산과 적용을 처리 했다. 이러한 minimize()함수를 다음과 같이 두 가지 함수로 분리할 수 있다.
옵티마이저의
compute_gradients()함수를 이용해 먼저 그래디언트를 계산한다.옵티마이저의
apply_gradients()함수에tf.clip_by_value()를 적용하여 클리핑된 그래디언트를 적용한다.
################
# layer params #
################
n_inputs = 28*28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10
# input layer
inputs = tf.placeholder(tf.float32, shape=[None, n_inputs], name="X")
# output layer
labels = tf.placeholder(tf.int32, shape=[None], name='labels')
with tf.name_scope('dnn'):
hidden1 = tf.layers.dense(inputs, n_hidden1, activation=tf.nn.relu, name="hidden1")
hidden2 = tf.layers.dense(hidden1, n_hidden2, activation=tf.nn.relu, name='hidden2')
logits = tf.layers.dense(hidden2, n_outputs, name='logits')
with tf.name_scope('loss'):
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits)
loss = tf.reduce_mean(xentropy, name='loss')
################
# Hyper-params #
################
learning_rate = 0.01
threshold = 1.0
n_epochs = 5
batch_size = 50
with tf.name_scope('train'):
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
# 그래디언트 계산
grad_and_vars = optimizer.compute_gradients(loss)
# 그래디언트 클리핑
clipped_grads = [(tf.clip_by_value(grad, -threshold, threshold), var)
for grad, var in grad_and_vars]
# 클리핑 된 그래디언트 적용
train_op = optimizer.apply_gradients(clipped_grads)
with tf.name_scope('eval'):
correct = tf.nn.in_top_k(logits, labels, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
with tf.Session() as sess:
tf.global_variables_initializer().run()
for epoch in range(n_epochs):
for batch_x, batch_y in shuffle_batch(train_x, train_y, batch_size):
sess.run(train_op, feed_dict={inputs: batch_x,
labels:batch_y})
# validation
accuracy_val = accuracy.eval(feed_dict={inputs: valid_x, labels: valid_y})
print('epoch: {:03d}, valid. Acc: {:.4f}'.format(epoch, accuracy_val))
"""
epoch: 000, valid. Acc: 0.9026
epoch: 001, valid. Acc: 0.9244
epoch: 002, valid. Acc: 0.9362
epoch: 003, valid. Acc: 0.9410
epoch: 004, valid. Acc: 0.9460
"""3. 마무리
이번 포스팅에서는 심층 신경망 학습 단계에서 그래디언트 소실/폭주 문제를 감소시키는 기법인 배치 정규화(Batch Normalization)와 그래디언트 클리핑(Graident Clipping)에 대해 알아보았다.
위의 코드에 대한 전체 코드는 https://github.com/ExcelsiorCJH/Hands-On-ML/blob/master/Chap11-Training_DNN/Chap11_2-Training_DNN.ipynb
'DeepLearning > 개념' 카테고리의 다른 글
| 07-1.순환 신경망(RNN, Recurrent Neural Network) - (1) (2) | 2018.10.25 |
|---|---|
| 06. 합성곱 신경망 - Convolutional Neural Networks (8) | 2018.10.19 |
| 05-1. 심층 신경망 학습 - 활성화 함수, 가중치 초기화 (4) | 2018.10.05 |
| 04. 인공신경망 - Artificial Neural Networks (2) | 2018.09.13 |
| 03. 오차역전파 - BackPropagation (0) | 2018.09.12 |